题目内容
如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠ABC=∠CAD.
(1)若∠ABC=20°,则∠OCA的度数为 ;
(2)判断直线AD与⊙O的位置关系,并说明理由;
(3)若OD⊥AB,BC=5,AB=8,求⊙O的半径.
 |
解:(1)70°;…………2分.
 (2)相切
(2)相切
理由如下:法一:连接OA,∠ABC=![]() ∠AOC……3分.
∠AOC……3分.
在等腰△AOC中,∠OAC=90°-![]() ∠AOC
∠AOC
∴∠OAC=90°-∠ABC ……4分.
∵∠ABC=∠CAD,
∴∠OAD=∠OAC+∠CAD=90°-∠ABC+∠ABC=90°……5分.
即OA⊥AD,而点A在⊙O上,∴直线AD与⊙O相切.…………6分.
法二:连接OA,并延长AO与⊙O相交于点E,连接EC.
∵AE是⊙O的直径,∴∠ECA=90°,…………3分.
∴∠EAC+∠AEC=90°.
又∵∠ABC=∠AEC,∠ABC=∠CAD,∴∠EAC+∠CAD=90°.……5分.
即OA⊥AD,而点A在⊙O上,∴直线AD与⊙O相切.…………6分.
(3)设OD与AB的交点为点G.
∵OD⊥AB,∴AG=GB=4. AC=BC=5,在Rt△ACG中,可得GC=3.…………7分.
在Rt△OGA中,设OA=x,由OA2=OG2+AG2,得x2=(x-3)2+42……9分.
解得x=![]() ,即⊙O的半径为
,即⊙O的半径为![]() . …………10分.
. …………10分.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
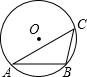 如图,已知△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为
如图,已知△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为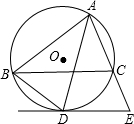 如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.
如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E. (2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N. 如图,已知△ABC内接于⊙O,AE平分∠BAC,且AD⊥BC于点D,连接OA.
如图,已知△ABC内接于⊙O,AE平分∠BAC,且AD⊥BC于点D,连接OA. 如图,已知△ABC内接于⊙O,AB=AC,∠A=36°,CD是⊙O的直径,求∠ACD的度数.
如图,已知△ABC内接于⊙O,AB=AC,∠A=36°,CD是⊙O的直径,求∠ACD的度数.