题目内容
16.解方程:(1)2x2-x-3=0
(2)(y-3)2+4y(y-3)=0.
分析 (1)把方程左边式子进行因式分解得到(2x-3)(x+1)=0,再解两个一元一次方程即可;
(2)提取公因式(y-3)得到(y-3)(5y-3)=0,再解两个一元一次方程即可.
解答 解:(1)∵2x2-x-3=0,
∴(2x-3)(x+1)=0,
∴x+1=0或2x-3=0,
∴x1=-1,x2=$\frac{3}{2}$;
(2)∵(y-3)2+4y(y-3)=0,
∴(y-3)(y-3+4y)=0,
∴(y-3)(5y-3)=0,
∴5y-3=0或y-3=0,
∴y1=$\frac{3}{5}$,y2=3.
点评 本题考查了因式分解法解一元二次方程,当把方程通过移项把等式的右边化为0后方程的左边能因式分解时,一般情况下是把左边的式子因式分解,再利用积为0的特点解出方程的根.因式分解法是解一元二次方程的一种简便方法,要会灵活运用.

练习册系列答案
相关题目
11.在平面直角坐标系中,点P在第四象限,且点P到x轴的距离是3,到y轴的距离是2,则点P的坐标为( )
| A. | (-2,3) | B. | (-3,2) | C. | (3,2) | D. | (2,-3) |
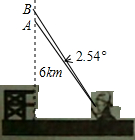 如图,一只运载火箭从地面L处发射,当卫星到达A点时,从位于地面R处的雷达站测得AR的距离是6km,仰角为43°,1s后,火箭到达B点,此时测得仰角为45.54°,这个火箭从A到B的平均速度是多少(精确到0.01km/s)?
如图,一只运载火箭从地面L处发射,当卫星到达A点时,从位于地面R处的雷达站测得AR的距离是6km,仰角为43°,1s后,火箭到达B点,此时测得仰角为45.54°,这个火箭从A到B的平均速度是多少(精确到0.01km/s)? 如图,平面内有公共端点的八条射线0A,OB,OC,OD,OE,OF,OG,OH,从射线OA开始般逆时针方向依次在射线上写除数字1,2,3,4,5,6,7,8…
如图,平面内有公共端点的八条射线0A,OB,OC,OD,OE,OF,OG,OH,从射线OA开始般逆时针方向依次在射线上写除数字1,2,3,4,5,6,7,8…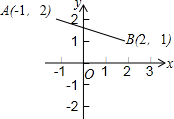 已知平面直角坐标系中,A(-1,2),B(2,1),线段AB交y轴于C点
已知平面直角坐标系中,A(-1,2),B(2,1),线段AB交y轴于C点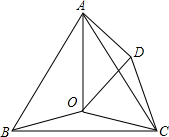 如图,点O是等边△ABC内一点,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OA和OD.
如图,点O是等边△ABC内一点,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OA和OD. 如图,在△ABC中,∠A=40°,有一块直角三角板DEF的两条直角边DE、DF分别经过点B、C,若直角顶点D在三角形外部,则∠ABD+∠ACD的度数是230度.
如图,在△ABC中,∠A=40°,有一块直角三角板DEF的两条直角边DE、DF分别经过点B、C,若直角顶点D在三角形外部,则∠ABD+∠ACD的度数是230度. 如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,延长BC到E,使得CE=AD,连接DE.
如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,延长BC到E,使得CE=AD,连接DE.