题目内容
19. 如图,点A是反比例函数y=$\frac{1}{x}$(x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比函数图象上移动时,点B也在某一反比例函数图象y=$\frac{k}{x}$上移动,k的值为( )
如图,点A是反比例函数y=$\frac{1}{x}$(x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比函数图象上移动时,点B也在某一反比例函数图象y=$\frac{k}{x}$上移动,k的值为( )| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
分析 过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,易得△AOC∽△OBD,由相似三角形面积比等于相似比的平方,求得S△AOC:S△BOD,继而求得答案.
解答  解:过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
解:过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
∴∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠BOD=∠OAC,
∴△AOC∽△OBD,
∴S△AOC:S△BOD=($\frac{OA}{OB}$)2,
∵OB=2OA,
∴S△AOC:S△BOD=$\frac{1}{4}$,
∵S△AOC=$\frac{1}{2}$OC•AC=$\frac{1}{2}$×1=$\frac{1}{2}$,S△BOD=$\frac{1}{2}$OD•BD=$\frac{1}{2}$|k|,
∴k=-4,
故选D.
点评 此题考查了待定系数法求反比例函数的解析式,相似三角形的判定与性质以及反比例函数的性质,掌握辅助线的作法是解题的关键,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
10.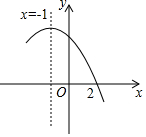 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )
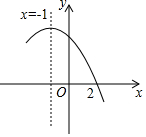 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
2.下列分数中,不能化为有限小数的是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |