Question

【题目】如图，在每个小正方形的边长为1的网格中，的顶点A，B，O均落在格点上，为⊙O的半径．

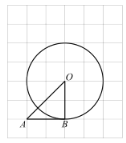
（1）的大小等于_________（度）；

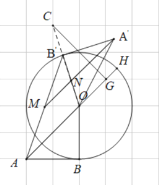
（2）将绕点O顺时针旋转，得，点A，B旋转后的对应点为，．连接，设线段的中点为M，连接．当取得最大值时，请在如图所示的网格中，用无刻度的直尺画出点，并简要说明点的位置是如何找到的（不要求证明）．

Answer 1

【答案】（1）45；（2）取 的中点N，连接MN，，构成，延长AO交⊙O于点H，在OH上取格点G，取格点C，连接OC与⊙O交于．

【解析】

（1）由图可知，△ABO是等腰直角三角形，即可求出的度数；

（2）当过的中点时，取得最大值，由点M，N分别是的中点，可得，根据网格的特点，作即可画出点．

解：（1） 由图形可知，OA=OB，OB⊥OA，

∴△ABO是等腰直角三角形，

∴，

故答案为：45；

（2）取 的中点N，连接MN，，构成，延长AO交⊙O于点H，如图，

根据三角形三边关系，,

当点，N，M三点共线时，取最大值，

在中，，

∵点M，N分别是的中点，

∴，

作，由网格图的特点可得，

在OH上取格点G，取格点C，连接OC与⊙O交于，如图所示，

，此时，，

故连接OC与⊙O交于，点即为所求．