题目内容
18.直线y=$\frac{4}{3}$x+4交x轴于A,交y轴于B.求:∠ABO的余切、正弦.分析 首先求出A,B点坐标,进而得出AO,BO,AB的长,再利用锐角三角函数关系求出即可.
解答 解:∵直线y=$\frac{4}{3}$x+4交x轴于A,交y轴于B,
∴y=0时,$\frac{4}{3}$x+4=0,解得:x=-3,
x=0时,y=4,则A(-3,0),B(0,4),
则AO=3,BO=4,
在Rt△AOB中,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
sin∠ABO=$\frac{AO}{AB}$=$\frac{3}{5}$,
cot∠ABO=$\frac{OB}{OA}$=$\frac{4}{3}$.
点评 此题主要考查了一次函数图象上点的坐标性质以及锐角三角函数定义,得出三角形各边长是解题关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
7.考虑下面两种宽带网的收费方式:
设月上网时间为xh.
(Ⅰ)用含有x的式子填写表格:
(Ⅱ)在某种上网时间下,两种收费方式能否相等?如果能,这时的上网时间是多少?如果不能,说明理由.
| 收费方式 | 月使用费(元) | 包时上网时间(h) | 超时费(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
(Ⅰ)用含有x的式子填写表格:
| 0≤x<25 | 25<x≤50 | x>50 | |
| 收费方式A应收取费用(元) | 30 | 3x-45 | 3x-45 |
| 收费方式B应收取费用(元) | 50 | 50 | 3x-100 |
10. 如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
 如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )
如图,正方形ABCD的四个顶点分别在四条平行线l1,l2,l3,l4上,AD,BC边分别与l2,l3相交于点F,E,这四条直线中相邻两条之间的距离依次为a,b,c(a>0,b>0,c>0),且AB边于直线l2的夹角为α,则下列结论错误的是( )| A. | a=c | B. | 当a=b=c时,四边形BEDF是菱形 | ||
| C. | $\frac{AF}{AB}$=$\frac{a}{a+b}$ | D. | 正方形ABCD面积为(a+b)2+c2 |
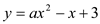 (
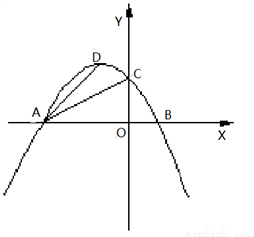
(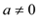 )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .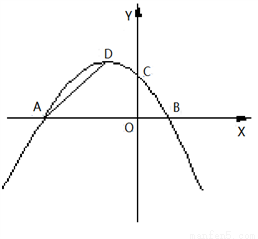

 1×
1× =1-
=1-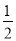
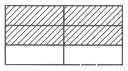
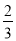 =2-
=2-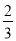
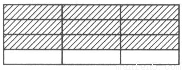
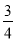 =3-
=3-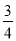

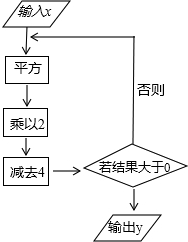 根据如图所示的程序计算.
根据如图所示的程序计算.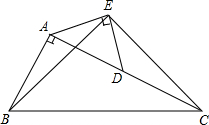 已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.
已知:如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,以AD为斜边在△ABC外作等腰直角三角形AED,连结BE、EC.试猜想线段BE和EC有何关系,并证明你的猜想.