题目内容
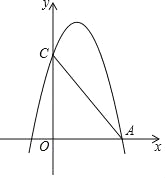
【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0）和点B，与y轴交于点C，点C关于抛物线对称轴的对称点为点D，抛物线顶点为H（1，2）．
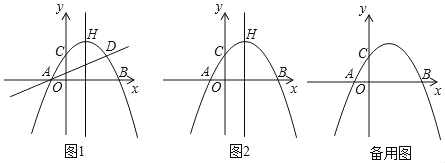
（1）求抛物线的解析式；
（2）点P为直线AD上方抛物线的对称轴上一动点，连接PA，PD．当S△PAD=3，若在x轴上存在一动点Q，使PQ+
QB最小，求此时点Q的坐标及PQ+QB的最小值；
（3）若点E为抛物线上的动点，点G，F为平面内的点，以BE为边构造以B，E，F，G为顶点的正方形，当顶点F或者G恰好落在y轴上时，求点E的横坐标．
【答案】（1）y=﹣
x2+x+
；（2）
；（3）
或1+
或2+
．
【解析】
（1））由抛物线的顶点为H（1，2），可以假设抛物线的解析式为y=a（x-1）2+2，把A（-1，0）代入得到，a=-；
（2）如图1中，连接PA，PD，在y轴上取一点M（0，-），连接BM，作QN⊥BM于N．设AD交对称轴于K．首先证明QN=
BQ，推出PQ+BQ=PQ+QN，根据垂线段最短可知，当HN⊥BM，且P，Q，N共线时，PQ+BQ的值最小，最小值=线段PN的值；
（3）设P（m，-m2+m+3），有三种情况：①如图2，当G在y轴上时，过E作EQ⊥y轴于Q，作EM⊥x轴于M，证明△EQG≌△EMB，则EQ=EM，列方程可得m的值；②当F在y轴上时，如图3，过E作EM⊥x轴于M，同法可得；③当G在y轴上时，如图4，作EM⊥OB于E，EN⊥OG于N．只要证明EM=EN，构建方程即可解决问题.
（1）∵抛物线的顶点为H（1，2），
∴可以假设抛物线的解析式为y=a（x﹣1）2+2，
把A（﹣1，0）代入得到，a=﹣，
∴抛物线的解析式为y=﹣（x﹣1）2+2，即y=﹣x2+x+；
（2）如图1中，连接PA，PD，在y轴上取一点M（0，﹣），连接BM，作QN⊥BM于N．设AD交对称轴于K，
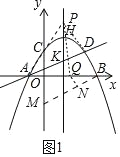
由题意C（0，），D（2，），A（﹣1，0），B（3，0），
∴直线AD的解析式为y=x+,，
∴K（1，1），设P（1，m），
则有×（m﹣1）×3=3，
∴m=3，
∴P（1，3），
∵OB=3，OM=，
∴BM=
，
∴sin∠ABM=
=，
∴
=，
∴QN=BQ，
∴PQ+BQ=PQ+QN，
根据垂线段最短可知，当HN⊥BM，且P，Q，N共线时，PQ+BQ的值最小，最小值=线段PN的值,
∵直线BM的解析式为y=x﹣，
∴当PN⊥BM时，直线PN的解析式为y=﹣2x+5，此时Q（3，0），
由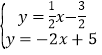
，解得
，
∴N（
，﹣
），
∴PN=
=，
∴PQ+BQ的最小值为；
（3）设F（m，﹣m2+m+），
有三种情况：
①如图2，当G在y轴上时，过E作EQ⊥y轴于Q，作EM⊥x轴于M，
∵四边形EBFG是正方形，
∴EG=EB，
∵∠EQG=∠EMB=90°，∠QEG=∠MEB，
∴△EQG≌△EMB，
∴EQ=EM，
即m=﹣m2+m+，
解得：m1=，m2=﹣（舍），
∴E的横坐标为；
②当F在y轴上时，如图3，过E作EM⊥x轴于M，
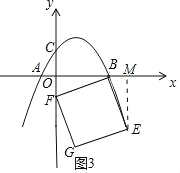
同理得：△EMB≌△BOF，
∴OB=EM=3，
即﹣m2+m+=﹣3，
m1=1﹣（舍），m2=1+，
∴E的横坐标为1+；
③当G在y轴上时，如图4，作EM⊥OB于E，EN⊥OG于N，
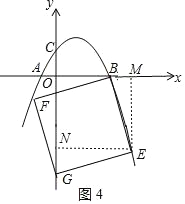
同法可证：EN=EM，
∴m=﹣（﹣m2+m+），
解得m1=2+，m2=2﹣（舍弃），
∴点E的横坐标为2+
综上所述，点E的横坐标为或1+或2+．
