题目内容
17．已知∠A为锐角，且tanA=$\frac{2}{3}$，那么下列判断正确的是（ ）| A． | 0＜∠A＜30° | B． | 30°＜∠A＜45° | C． | 45°＜∠A＜60° | D． | 60°＜∠A＜90° |
分析 根据正切函数的增减性，可得答案．
解答 解：$\frac{\sqrt{3}}{3}$＜$\frac{2}{3}$＜1，
由正切函数随锐角的增大而增大，得
tan30°＜tanA＜tan45°，
即30°＜A＜45°，
故选：B．
点评 本题考查了特殊角的三角函数值，利用正切函数的增减性是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$的图象相交于A，B两点，其中点A的坐标为（$\sqrt{3}$，2$\sqrt{3}$）．
12．计算：3$\sqrt{12}$÷3$\sqrt{\frac{1}{3}}$-2$\sqrt{3}$的结果为（ ）
| A． | -2$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | 6-2$\sqrt{3}$ | D． | 36-2$\sqrt{3}$ |
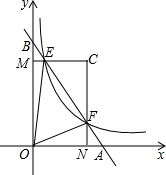在直角坐标系中，直线AB与x轴，y轴分别交于点A，B，与反比例函数y=$\frac{k}{x}$（k为常数，且k＞0）在第一象限的图象交于点E，F，过E作EM⊥y轴于M，过点F作FN⊥x轴于N，直线EM与FN交于点C．