题目内容
两个图形成中心对称和中心对称图形有什么区别？
见解析
【解析】【试题分析】注意区分好成中心对称和中心对称图形的定义.
【试题解析】
前者是指具有某种特性（绕一点旋转180度后能与原图重合）的一个图形；后者是指两个图形之间，若其中某一个图形绕一点旋转180度后能与另一个图形重合，则称这两个图形之间成中心对称.
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
如图，将边长为8㎝的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在F处，折痕为MN，则线段CN的长是（ ）
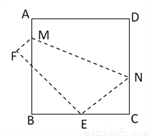
A. 3cm B. 4cm C. 5cm D. 6cm
A
【解析】分析：根据折叠的性质，只要求出DN就可以求出NE，在直角△CEN中，若设CN=x，则DN=NE=8-x，CE=4cm，根据勾股定理就可以列出方程，从而解出CN的长．
解答：【解析】
设CN=xcm，则DN=（8-x）cm，由折叠的性质知EN=DN=（8-x）cm，
而EC=BC=4cm，在Rt△ECN中，由勾股定理可知EN2=EC2+CN2，即（8-x）2=16+x... 某单位要在两名射击队员中推出一名参加比赛，已知同等条件下，甲射中某物的可能性大于乙，则所推出的人中应（ ）
A. 选甲 B. 选乙 C. 都可以 D. 不能确定
A
【解析】根据题意可知，同等条件下，甲射中某物的可能性大于乙.故应该派甲去.
故选A. 如图，在△ABC中，∠ACB＝90°，D是BC延长线上一点，E是BD垂直平分线与AB的交点，DE交AC于点F.求证：点E在AF的垂直平分线上．
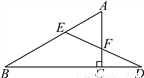
见解析
【解析】试题分析：过E作EG垂直于AC，交AC于G，可得出EG∥BD故∠AEG=∠B，∠D=∠DEG．再根据E是BD的垂直平分线与AB的交点可得出∠B=∠D，根据ASA定理得出△AEG≌△FEG，进而可得出结论．
试题解析：
证明：如图所示：
过E作EG垂直于AC，交AC于G，
∵∠ACB=90°，
∴EG∥BD，
∴∠AEG=∠B，∠D=∠DEG．
∵... 如图，已知线段a、h，作等腰△ABC，使AB＝AC，且BC＝a，BC边上的高AD＝h.张红的作法是：①作线段BC＝a；②作线段BC的垂直平分线MN，MN与BC相交于点D；③在直线MN上截取线段h；④连接AB、AC，则△ABC为所求的等腰三角形．上述作法的四个步骤中，你认为有错误的一步是( )
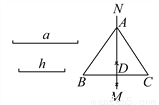
A. ① B. ② C. ③ D. ④
C
【解析】在直线MN上截取线段h，带有随意性，与作图语言的准确性不相符．
故选C． 判断对错：两个会重合的图形一定是中心对称图形； ___________
错
【解析】两个会重合的图形不一定是中心对称图形，因为还要看是否存在对称中心.
故答案：错. 在下列图形中，是中心对称图形的是( )
A. 
B. 
C. 
D. 
C
【解析】试题分析：A、旋转180°后不能与自身重合，不是中心对称图形；
B、旋转180°后不能与自身重合，不是中心对称图形；
C、旋转180°后能与自身重合，是中心对称图形；
D、旋转180°后不能与自身重合，不是中心对称图形．
故选C． 已知a+
=3，则a2+
的值是_____．
7
【解析】试题分析：把已知条件两边平方，然后整理即可求解．∵=3，∴=9，∴=9﹣2=7．
故答案为：7． 在平面直角坐标系中，点P（-1，2）向右平移3个单位长度得到的点的坐标是 ______ ．
（2，2）．
【解析】试题分析：点P（﹣1，2）向右平移3个单位长度得到的点的坐标是（﹣1+3，2），即（2，2）．故答案为：（2，2）．