题目内容
1.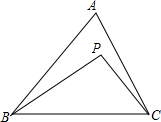 如图,点P是△ABC内的一点,有下列结论:①∠BPC>∠A;②∠BPC一定是钝角;③∠BPC=∠A+∠ABP+∠ACP.其中正确的结论为( )
如图,点P是△ABC内的一点,有下列结论:①∠BPC>∠A;②∠BPC一定是钝角;③∠BPC=∠A+∠ABP+∠ACP.其中正确的结论为( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
分析 连接AP并延长,根据三角形内角与外角的性质可得∠BPC=∠A+∠ABP+∠ACP,据此作出判断.
解答  解:连接AP并延长,如图1,则∠1是△ABP的外角,∠2是△APC的外角,
解:连接AP并延长,如图1,则∠1是△ABP的外角,∠2是△APC的外角,
故∠1=∠BAP+∠ABP,∠2=∠CAP+∠ACP,∠1>∠BAP,∠2>∠CAP,
即∠BPC=∠A+∠ABP+∠ACP,∠1+∠2>∠BAP+∠CAP,
即∠CPB>∠BAC,
故①③正确,
∠BPC可能是锐角,可能是直角,也可能是钝角,
故②错误.
故选C.
点评 本题考查的是三角形外角的性质,解答此题的关键是熟知以下知识:
①三角形的外角等于和它不相邻的两个内角的和;
②三角形的外角大于任一和它不相邻的内角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.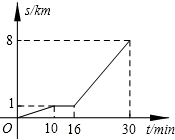 成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )
成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )
 成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )
成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )| A. | 他离家8千米,共用了30分钟 | B. | 他等公交车时间为6分钟 | ||
| C. | 他步行的速度是100米/分钟 | D. | 公交车的速度是350米/分钟 |
11.下列说法正确的是( )
| A. | 每个定理都有逆定理 | B. | 每个命题都有逆命题 | ||
| C. | 假命题没有逆命题 | D. | 真命题的逆命题是真命题 |
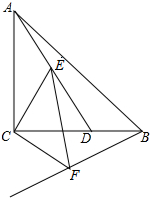 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC,D在BC上且∠BAD=15°,E是AD上的一点,现以CE为直角边,C为直角顶点在CE的下方作等腰直角三角形ECF,连接BF.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC,D在BC上且∠BAD=15°,E是AD上的一点,现以CE为直角边,C为直角顶点在CE的下方作等腰直角三角形ECF,连接BF.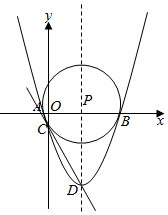 如图,已知二次函数y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为(4,0)或(4,$\frac{75}{8}$).
如图,已知二次函数y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为(4,0)或(4,$\frac{75}{8}$).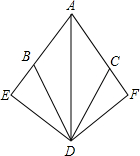 已知如图,BD=CD,∠ADB=∠ADC,DE、DF分别垂直于AB是AC交延长线于E、F.试问BE=CF吗?请说明理由.
已知如图,BD=CD,∠ADB=∠ADC,DE、DF分别垂直于AB是AC交延长线于E、F.试问BE=CF吗?请说明理由.