题目内容
（2012•路南区一模）在平面直角坐标系xOy中，以点（3，4）为圆心和y轴相切的⊙O1，以（6，0）为圆心，a为半径的⊙O2．若⊙O1与⊙O2相交，则a的取值范围（ ）
分析：首先根据题意，利用勾股定理即可求得O1O2的值，继而根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可求得答案．
解答：
解：如图，连接O1O2，过点O1作O1A⊥x轴，
∵O1（3，4），O2（6，0），
∴O1A=4，OA=3，O2A=6，
∴O2A=3，
∴O1O2=
=5，
∵以点（3，4）为圆心的⊙O1和y轴相切，
∴⊙O1的半径为3，
∵⊙O1与⊙O2相交，
∴a-3＜5＜a+3，
∴2＜a＜8．
故选C．
解：如图，连接O1O2，过点O1作O1A⊥x轴，∵O1（3，4），O2（6，0），
∴O1A=4，OA=3，O2A=6，
∴O2A=3，
∴O1O2=
| O1A2+O2A2 |
∵以点（3，4）为圆心的⊙O1和y轴相切，
∴⊙O1的半径为3，
∵⊙O1与⊙O2相交，
∴a-3＜5＜a+3，
∴2＜a＜8．
故选C．
点评：此题考查了圆与圆的位置关系．此题难度适中，注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系，注意数形结合思想的应用．
练习册系列答案
相关题目
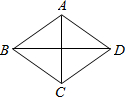（2012•路南区一模）如图，在菱形ABCD中，两条对角线AC=12，BD=16，则此菱形的边长为（ ）
（2012•路南区一模）如图，将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE∥BC，下列结论中一定正确的是（ ）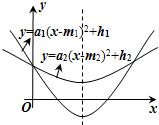
（2012•路南区一模）如图，直角坐标系中，两条抛物线有相同的对称轴，下列关系中不正确的是（ ）
（2012•路南区一模）如图，在水平桌面上有甲、乙两个内部呈圆柱形的容器，内部底面积分别为80cm2、100cm2，且甲容器装满水，乙容器是空的．若将甲中的水全部倒入乙中，则乙中的水位高度比原先甲的水位高度低了8cm，设甲容器的容积为x cm3，则根据题意得（ ）