题目内容
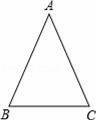
如图,在△ABC中,∠B=∠C=67.5°.
(Ⅰ)求sinA的值;
(Ⅱ)求tanC的值.

【考点】解直角三角形.
【专题】探究型.
【分析】(1)要求sinA的值,根据三角形内角和可求得∠A的度数,从而可以求得sinA的值;
(2)要求tanC的值,只要作辅助线BD⊥AC于点D,然后通过变形,即可求得tanC的值.
【解答】解:(1)∵在△ABC中,∠B=∠C=67.5°,
∴∠A=180°﹣∠B﹣∠C=180°﹣67.5°﹣67.5°=45°,
∴sinA=sin45°=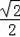
 ,
,
即sinA=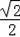
 ;
;
(2)作BD⊥AC于点D,如下图所示,
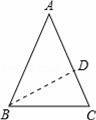

∵由(1)可知∠A=45°,设BD=a,
∴AD=a,AB=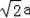
 ,
,
∵AB=AC,
∴AC=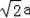
 ,
,
∴CD=AC﹣AD=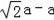
 ,
,
∴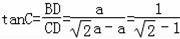
 =
=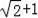
 ,
,
即tanC=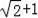
 .
.
【点评】本题考查解直角三角形、三角形的内角和、求角的三角函数值,解题的关键是明确题意,找出对应量,求出相应的三角函数值.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目


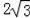
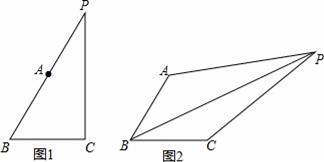


 B.
B.
 C.
C.
 D.
D.




 的解集是( )
的解集是( )