题目内容
如图平面直角坐标系中,点A(1,n)和点B(m,1)为双曲线y= 第一象限上两点,连结OA、OB.
第一象限上两点,连结OA、OB.
(1)试比较m、n的大小;
(2)若∠AOB=30°,求双曲线的解析式.
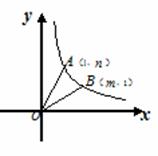
解:( 1)∵点A(1,
1)∵点A(1, )和点B(
)和点B( ,1)为双曲线
,1)为双曲线 上的点,
上的点,
∴ .
.
∴ =
= =
= . ……2分
. ……2分
(2)过A作AC⊥y轴于C,过B作BD⊥x轴于D,
则∠ACO=∠BDO=90°, AC=1,OC=
AC=1,OC= ,BD=1,OD=
,BD=1,OD= ,
,
∴AC=OC.
∵ =
= ,∴OC=OD,AC=OC,
,∴OC=OD,AC=OC,
∴△ACO≌△BDO,
∴∠AOC=∠BOD= (∠COD-∠AOB)=
(∠COD-∠AOB)= (90°-30°)=30°.
(90°-30°)=30°.
 ∵在Rt△AOC中,tan∠AOC=
∵在Rt△AOC中,tan∠AOC= ,
,
∴OC= ,
,
∴点A的坐标为(1, ).
).
∵点A(1, )为双曲线
)为双曲线 上的点,
上的点,
∴ , ∴
, ∴  =
= .
.
∴反比例函数的解析式为 . ……6分
. ……6分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

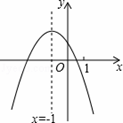
 向上平移3个单位长度,在向右平移1个单位长度后,得到的抛物线的解析式是 .
向上平移3个单位长度,在向右平移1个单位长度后,得到的抛物线的解析式是 .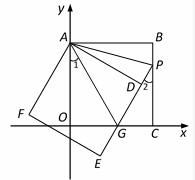

 )÷(﹣9)
)÷(﹣9)