Question

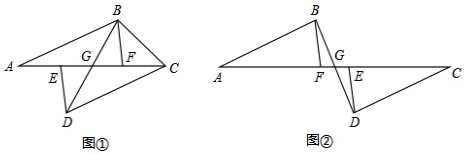
如图①所示，E、F分别为线段AC上的两个动点，且AB∥CD，若AB=CD，AF=CE，BD交AC于G点．
（1）求证：BF=DE，BF∥DE；
（2）当E、F两点移动到如图②所示的位置，其余条件不变，上述结论是否成立？并说明理由．

Answer 1

分析：（1）由AB∥CD，可得∠A=∠DCE，又由AB=CD，AF=CE，可利用SAS证得△ABF≌△CD，继而证得结论；
（2）同（1），可利用SAS证得△ABF≌△CD，继而证得结论．

解答：（1）证明：∵AB∥CD，
∴∠A=∠DCE，
在△ABF和△CDE中，

AB=CD ∠A=∠DCE AF=CE

，
∴△ABF≌△CDE（SAS），
∴BF=DE，∠BFA=∠DEC，
∴BF∥DE；

（2）解：成立．
理由：∵AB∥CD，
∴∠A=∠C，
在△ABF和△CDE中，

AB=CD ∠A=∠C AF=CE

，
∴△ABF≌△CDE（SAS），
∴BF=DE，∠BFA=∠DEC，
∴BF∥DE．

点评：此题考查了全等三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．