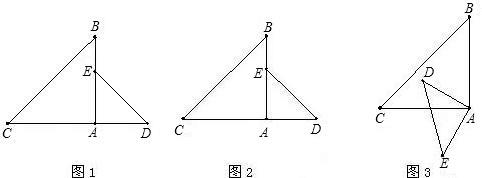
题目内容
(1)如图1所示,BD,CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别为F,G,连结FG,延长AF,AG,与直线BC分别交于点M、N,那么线段FG 与△ABC的周长之间存在的数量关系是什么?即:FG=____(AB+BC+AC)(直接写出结果即可)
(2)如图2,若BD,CE分别是△ABC的内角平分线;其他条件不变,线段FG与ΔABC三边之间又有怎样的数量关系?请写出你的猜想,并给予证明。
(3)如图3,若BD为△ABC的内角平分线,CE为△ABC的外角平分线,其他条件不变,线段FG与ΔABC三边又有怎样的数量关系?直接写出你的猜想即可。不需要证明。
(2)如图2,若BD,CE分别是△ABC的内角平分线;其他条件不变,线段FG与ΔABC三边之间又有怎样的数量关系?请写出你的猜想,并给予证明。
(3)如图3,若BD为△ABC的内角平分线,CE为△ABC的外角平分线,其他条件不变,线段FG与ΔABC三边又有怎样的数量关系?直接写出你的猜想即可。不需要证明。

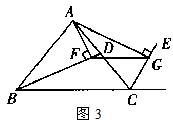
解:(1)FG=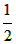 (AB+BC+AC); (AB+BC+AC); |
|
(2)FG=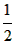 (AB+AC-BC); (AB+AC-BC);证明:延长AG交BC于N,延长AF交BC于M, ∵AF⊥BD,AG⊥CE, ∴∠AGC=∠CGN=90°,∠AFB=∠BFM=90°, 在RtΔAGC和RtΔCGN中, ∠AGC=∠CGN=90°,CG=CG,∠ACG=∠NCG, ∴RtΔAGC≌RtΔCGN, ∴AC=CN,AG=NG, 同理可证:AF=FM,AB=BM, ∴GF是ΔAMN的中位线, ∴GF= 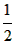 MN, MN,∵AB+AC=MB+CN=BN+MN+CM+MN,BC=BN+MN+CM, ∴AB+AC-BC=MN, ∴GF= 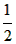 MN= MN=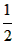 (AB+AC-BC); (AB+AC-BC); |
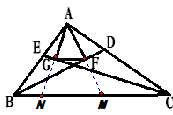 |
(3)线段FG与ΔABC三边之间数量关系是:GF=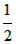 (AC+BC-AB)。 (AC+BC-AB)。 |

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目



 14、根据如图2所示的(1),(2),(3)三个图所表示的规律,依次下去第n个图中平行四边形的个数是
14、根据如图2所示的(1),(2),(3)三个图所表示的规律,依次下去第n个图中平行四边形的个数是
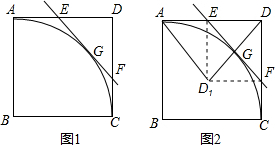 AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.
AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.