题目内容
 如图,在平面直角坐标系中,直线y=kx+5与x交于点A,与y交于点B,与抛物线y=ax2+bx交于点C、D.已知点C坐标为(1,7),点C横坐标为5.
如图,在平面直角坐标系中,直线y=kx+5与x交于点A,与y交于点B,与抛物线y=ax2+bx交于点C、D.已知点C坐标为(1,7),点C横坐标为5.(1)求直线与抛物线的解析式;
(2)将此抛物线沿对称轴向下平移几个单位,抛物线与直线AB一个交点.
考点:二次函数的性质,二次函数图象与几何变换
专题:计算题
分析:(1)先把C点坐标代入y=kx+5求出k得到直线解析式为y=2x+5,再利用直线解析式确定D点坐标,然后把C点和D点坐标分别代入y=ax2+bx得到关于a、b的方程组,解方程组求出a和b即可得到抛物线解析式;
(2)根据抛物线的平移问题,设将此抛物线沿对称轴向下平移b个单位,抛物线与直线AB一个交点,则平移后的抛物线为y=-x2+8x-b,把函数图象有一个交点转化为-x2+8x-b=2x+5有相等的实数解,然后利用根的判别式的意义得到△=(-6)2-4(b+5)=0,再解方程求出b即可.
(2)根据抛物线的平移问题,设将此抛物线沿对称轴向下平移b个单位,抛物线与直线AB一个交点,则平移后的抛物线为y=-x2+8x-b,把函数图象有一个交点转化为-x2+8x-b=2x+5有相等的实数解,然后利用根的判别式的意义得到△=(-6)2-4(b+5)=0,再解方程求出b即可.
解答:解:(1)∵直线y=kx+5过点C(1,7),
∴k+5=7,解得k=2,
∴直线解析式为y=2x+5,
当x=5时,y=2×5+5=15,则D点坐标为(5,15),
把C(1,7)和D(5,15)分别代入得
,解得
,
∴抛物线的解析式为y=-x2+8x;
(2)设平移后的抛物线为y=-x2+8x-b,
∵y=-x2+8x-b与直线AB一个交点,
∴-x2+8x-b=2x+5有相等的实数解,
整理得x2-6x+5+b=0,
∴△=(-6)2-4(b+5)=0,解得b=4,
即此抛物线沿对称轴向下平移4个单位,抛物线与直线AB一个交点.
∴k+5=7,解得k=2,
∴直线解析式为y=2x+5,
当x=5时,y=2×5+5=15,则D点坐标为(5,15),
把C(1,7)和D(5,15)分别代入得
|
|
∴抛物线的解析式为y=-x2+8x;
(2)设平移后的抛物线为y=-x2+8x-b,
∵y=-x2+8x-b与直线AB一个交点,
∴-x2+8x-b=2x+5有相等的实数解,
整理得x2-6x+5+b=0,
∴△=(-6)2-4(b+5)=0,解得b=4,
即此抛物线沿对称轴向下平移4个单位,抛物线与直线AB一个交点.
点评:主要考查了二次函数的性质:二次函数y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.也考查二次函数与几何变换和抛物线与直线的交点问题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
已知两圆的半径分别为一元二次方程x2-7x+12=0的二根,圆心距为2,则两圆位置关系为( )
| A、外离 | B、外切 | C、相交 | D、内切 |
 如图,把矩形ABCD沿EF对折,若∠1=50°,则∠FED等于( )
如图,把矩形ABCD沿EF对折,若∠1=50°,则∠FED等于( )| A、50° | B、80° |
| C、65° | D、115° |
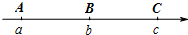 如图,数轴上的A、B、C三点所表示的数分别为a、b、c,其中AB=BC,如果点A到原点的距离最大,点B到原点的距离最小,那么该数轴的原点O的位置应该在( )
如图,数轴上的A、B、C三点所表示的数分别为a、b、c,其中AB=BC,如果点A到原点的距离最大,点B到原点的距离最小,那么该数轴的原点O的位置应该在( )| A、点A的左边 |
| B、点A与点B之间 |
| C、点B与点C之间 |
| D、点C的右边 |

 如图,直线a,b被直线l所截,a∥b,∠1=120°,∠3=
如图,直线a,b被直线l所截,a∥b,∠1=120°,∠3=