题目内容
 (1997•广州)如图,点B的坐标为(0,-2),点A在x轴正半轴上,将Rt△AOB绕y轴旋转一周,得到一个圆锥.
(1997•广州)如图,点B的坐标为(0,-2),点A在x轴正半轴上,将Rt△AOB绕y轴旋转一周,得到一个圆锥.(1)当圆锥的侧面积为
| 5 |
(2)若已知OA的长度为a,按这个圆锥的形状造一个容器,并在母线AB上刻出把这个容器的容积两等分的刻度点C,试用含a的代数式去表示BC的长度t(圆锥体积公式:V=
| 1 |
| 3 |
分析:(1)设点A的坐标为(x,0),求出AB,根据侧面积得出方程
•2xπ•
=
π,求出x,得出A的坐标,设直线AB的函数解析式为y=kx+b,把A、B的坐标代入求出即可;
(2)作CE⊥BO,垂足为E,根据面积得出EC2×BE=OA2=a2,①根据相似得出
=
,②由①、②求出EC=
,根据△EBC∽△OBA,推出
=
,即可求出答案.
| 1 |
| 2 |
| x2+4 |
| 5 |
(2)作CE⊥BO,垂足为E,根据面积得出EC2×BE=OA2=a2,①根据相似得出
| EC |
| BE |
| a |
| 2 |
| a | |||
|
| t |
| AB |
| EC |
| a |
解答:(1)解:设点A的坐标为(x,0),
则AB=
=
,
根据题意,得
•2xπ•
=
π,
解得:x=1,(x=-1不合题意,舍去),
设直线AB的函数解析式为y=kx+b,
把A(1,0),B(0,-2)分别代入上式得:
,
解得:k=2,b=-2,
∴直线AB的函数解析式为y=2x-2;
(2)解:作CE⊥BO,垂足为E,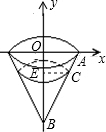
根据题意:
×
π×OA2×OB=
π×EC2×EB,
化简得:EC2×BE=OA2,
即EC2×EB=a2,①
∵△EBC∽△OBA,
∴
=
,②
由①、②,得
EC=
,
∵△EBC∽△OBA,
∴
=
,
∴t=
=
=
=
即t=
.
则AB=
| OA2+OB2 |
| x2+4 |
根据题意,得
| 1 |
| 2 |
| x2+4 |
| 5 |
解得:x=1,(x=-1不合题意,舍去),
设直线AB的函数解析式为y=kx+b,
把A(1,0),B(0,-2)分别代入上式得:
|
解得:k=2,b=-2,
∴直线AB的函数解析式为y=2x-2;
(2)解:作CE⊥BO,垂足为E,

根据题意:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
化简得:EC2×BE=OA2,
即EC2×EB=a2,①
∵△EBC∽△OBA,
∴
| EC |
| BE |
| a |
| 2 |
由①、②,得
EC=
| a | |||
|
∵△EBC∽△OBA,
∴
| t |
| AB |
| EC |
| a |
∴t=
| EC×AB |
| a |
=
EC•
| ||
| a |
=
| |||||||
| a |
=
| |||
|
即t=
| |||
| 2 |
| a2+4 |
点评:本题考查了勾股定理,圆锥的侧面积,相似三角形的性质和判定等知识点的应用,主要培养学生运用知识点进行计算和推理的能力,题目比较典型,但是有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
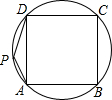 (1997•广州)如图,正方形ABCD内接于圆,点P在
(1997•广州)如图,正方形ABCD内接于圆,点P在
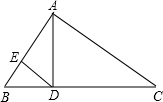 (1997•广州)如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,DE⊥AB,垂足为E,则图中与△ADE相似的三角形的个数为( )
(1997•广州)如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,DE⊥AB,垂足为E,则图中与△ADE相似的三角形的个数为( ) (1997•广州)如图,在Rt△ABC中,CD为斜边AB上的高,若AD=8,BD=4,则tanA=( )
(1997•广州)如图,在Rt△ABC中,CD为斜边AB上的高,若AD=8,BD=4,则tanA=( )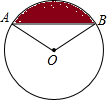 (1997•广州)如图,已知图中⊙O的半径为1,∠AOB=120°,则阴影部分的面积为( )
(1997•广州)如图,已知图中⊙O的半径为1,∠AOB=120°,则阴影部分的面积为( )