题目内容
（1997•广州）如图，在Rt△ABC中，CD为斜边AB上的高，若AD=8，BD=4，则tanA=（ ）分析：根据△ACD∽△CBD，可求出CD的长，然后在Rt△ACD中，可求出∠A的正切值．
解答：解：如图，在Rt△ABC中，CD是斜边AB上的高，∠ACB=∠CDB=90°，
又∵∠A=∠DCB，
∴△ACD∽△CBD，
∴
=
，
则CD2=AD•BD=8×4=32，
∴CD=4
，
∴tanA=
=
=
．
故选A．
又∵∠A=∠DCB，
∴△ACD∽△CBD，
∴
| AD |
| CD |
| CD |
| BD |
则CD2=AD•BD=8×4=32，
∴CD=4
| 2 |
∴tanA=
| CD |
| AD |
4
| ||
| 8 |
| ||
| 2 |
故选A．
点评：本题主要是掌握三角形相似的条件，以及三角函数的定义，是基础知识比较简单．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
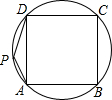（1997•广州）如图，正方形ABCD内接于圆，点P在
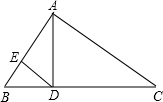（1997•广州）如图，在△ABC中，∠BAC=90°，AD⊥BC，垂足为D，DE⊥AB，垂足为E，则图中与△ADE相似的三角形的个数为（ ）
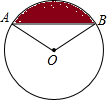（1997•广州）如图，已知图中⊙O的半径为1，∠AOB=120°，则阴影部分的面积为（ ）
（1997•广州）如图，点B的坐标为（0，-2），点A在x轴正半轴上，将Rt△AOB绕y轴旋转一周，得到一个圆锥．