题目内容

在我校“学风建设月”活动中，九（1）班同学掀起了学习的高潮，他们在学习数学中发现这样一个问题，若方程ax2+bx+c=0（a≠0）的两根为x1，x2，则x1+x2=-
b
a
，x1x2=
c
a
，并对此问题的证明展开了讨论．其中一同学的证法如下：设方程ax2+bx+c=0（a≠0）的两根为x1，x2，则有
x2-（x1+x2）x+x1x2=x2-
b
a
x+
c
a

a（x-x1）（x-x2）=ax2+bx+c
 x1+x2=-
b
a
   x1x2=
c
a

请仿此法，解答下列问题：设方程3x3-2x2+3x-1=0的根为x1，x2，x3，求x1x2+x1x3+x2x3的值．
考点：根与系数的关系
专题：阅读型
分析：根据题意，由方程3x3-2x2+3x-1=0的根为x1，x2，x3，那么原方程可写作：（x-x1）（x-x2）（x-x3）=0，运用多项式的乘法法则展开得：x3-（x1+x2+x3）x2+（x1x2+x1x3+x2x3）x-x1x2x3=0，而原等式两边同除以3得：x3-
2
3
x2+x-
1
3
=0，进而求出x1x2+x1x3+x2x3=1．
解答：解：∵方程3x3-2x2+3x-1=0的根为x1，x2，x3，
∴原方程可写作：（x-x1）（x-x2）（x-x3）=0，
展开得：x3-（x1+x2+x3）x2+（x1x2+x1x3+x2x3）x-x1x2x3=0，
而原等式两边同除以3得：x3-
2
3
x2+x-
1
3
=0，
∴x1x2+x1x3+x2x3=1．
点评：本题考查了根与系数的关系，学生的阅读理解能力及知识的迁移能力．读懂材料是解题的关键．
练习册系列答案
相关题目
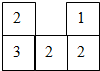如图所示是一个由若干个相同的小立方块所搭成的几何体从上面看到的图形，小正方形中的数字表示在该位置上小立方块的个数，请画出它从正面和从左面看到的平面图形．
已知⊙A的直径为8cm，且点B在⊙A上，那么AB=
 
cm．
已知：顺次连接矩形各边的中点，得到一个菱形，如图①；再顺次连接菱形各边的中点，得到一个新的矩形，如图②；然后顺次连接新的矩形各边的中点，得到一个新的菱形，如图③；如此反复操作下去，则第2012个图形中直角三角形的个数有
 
．
计算：
（1）-6+（-4）-（-2）（2）-16.8+8.4-3.2+2.6
（3）（-1
7
8
）-（-2
1
2
）+（-4
1
2
）-3
1
8
               
（4）（-
3
7
）×0.125×（-2
1
3
）×（-8）
（5）（29
12
13
）×（-26）
（6）（-30）×（
1
3
-
5
6
-
3
10
）
解下列方程
（1）x2+3x-2=0．                
（2）（2x-1）2=x（3x+2）-7．
把下列各数填在相应的大括号内．
5，-2，1.4，-
2
3
，-3.141，59，17
整数集合{              }
负分数集合{            }
非正数集合{            }
自然数集合{            }
非正整数集合{          }
有理数集合{            }．
阅读与应用
计算：
1
1×2
+
1
2×3
+
1
3×4
+…+
1
9×10

解：因为：
1
1×2
=1-
1
2
，
1
2×3
=
1
2
-
1
3
，
1
3×4
=
1
3
-
1
4
，…
1
9×10
=
1
9
-
1
10

所以：
1
1×2
+
1
2×3
+
1
3×4
+…+
1
9×10
=（1-
1
2
）+（
1
2
-
1
3
）+（
1
3
-
1
4
）+…+（
1
9
-
1
10
）=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
…+
1
9
-
1
10
=1-
1
10
=
9
10

计算：①
1
1×2
+
1
2×3
+
1
3×4
+…+
1
2004×2005

②
1
1×3
+
1
3×5
+
1
5×7
+…+
1
49×51
．
下列各选项正确的是（　　）
A、0.10（精确到0.1）
B、0.05（精确到十分位）
C、5.5万（精确到千位）
D、1.205×107（精确到0.001）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网