题目内容
若a是x2-3x+1=0的解，则a3-8a+3= ．
考点：一元二次方程的解
专题：
分析：直接解方程求出a的值，再代入求代数式的值，是一种基本思路．但这种思路比较麻烦．另外一种思路是由已知得到：a2-3a+1=0即a2-3a=-1用a2-3a把已知的式子表示出来，从而求代数式的值．
解答：解：由a是方程x2-3x+1=0的一个根得：a2-3a+1=0，即a2-3a=-1，
∴a3-8a+3=a3-3a2+3a2-a-a+3=a（a2-3a）+3（a2-3a）+a+3=-a-3+a+3=0．
故答案为：0．
∴a3-8a+3=a3-3a2+3a2-a-a+3=a（a2-3a）+3（a2-3a）+a+3=-a-3+a+3=0．
故答案为：0．
点评：本题考查了一元二次方程的解，解决求代数式的值的问题有两种思路：一种是直接解方程求出a的值，再代入求代数式的值；第二种是把所求的式子用已知的式子表示出来．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
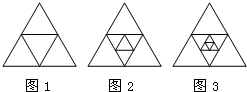如图，在图1中，互不重叠的三角形共有4个，在图，2中，互不重叠的三角形共有7个，在图3中，互不重叠的三角形共有10个，…，则在第9个图形中，互不重叠的三角形共有下列方程中有两个相等的实数根的方程是（ ）
| A、x2+2x=0 |
| B、x2+2ax+a2=0 |
| C、x2-4x-4=0 |
| D、ax2+2ax+a=0 |