Question

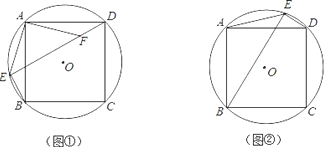
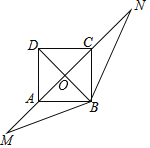
【题目】如图，在矩形ABCD中，BD⊥AC，对角线AC所在的直线上有两点M、N，使∠MBN＝135°，若AD＝4，AM＝3，则CN的长是_____．

Answer 1

【答案】

【解析】

先证明四边形ABCD是正方形，可得∠ABC＝90°，∠MBN＝135°，所以∠ABM+∠CBN＝45°，根据∠ACB＝45°，由三角形外角的性质得到∠CBN+∠N＝45°，所以∠ABM＝∠N 同理可得∠BMA＝∠CBN，所以△BMA～△NBC，根据三角形相似的性质可求得AMCN＝BCAB，则答案可求．

解：∵矩形ABCD中，BD⊥AC，

∴四边形ABCD是正方形，

∴AD＝BC＝AB＝4，∠ABC＝90°，

∵∠MBN＝135°，

∴∠ABM+∠CBN＝45°，

∵∠ACB＝∠CBN+∠N＝45°，

∴∠ABM＝∠N，同理∠BMA＝∠CBN，

∴△BMA∽△NBC，

∴

∴，

∴CN＝，

故答案为：．