题目内容
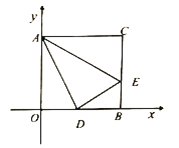
【题目】如图,在平面直角坐标系![]() 中,四边形
中,四边形![]() 为边长为6的正方形,点
为边长为6的正方形,点![]() 为
为![]() 的中点,
的中点,![]() .动点
.动点![]() 在线段
在线段![]() 和
和![]() 上运动,另一动点
上运动,另一动点![]() 在线段
在线段![]() 上运动.
上运动.
用学过的知识解决下列问题:
(1)①填空:点![]() 的坐标____________________;
的坐标____________________;
②求三角形![]() 的面积;
的面积;
(2)求点![]() 在运动过程中,
在运动过程中,![]() 与
与![]() 的数量关系;
的数量关系;
(3)两个动点![]() 在运动过程中,是否存在使线段
在运动过程中,是否存在使线段![]() 的长等于2的时刻,如果存在,求出此时点
的长等于2的时刻,如果存在,求出此时点![]() 坐标;如果不存在,请你说明理由.
坐标;如果不存在,请你说明理由.
【答案】(1)①![]() ;②9;(2)
;②9;(2)![]() 或
或![]() ;(3)
;(3)![]() 点坐标为
点坐标为![]() 或
或![]() .
.
【解析】
(1)由正方形边长和![]() ,求出BE长即可得到点E坐标. 由D是OB的中点可得OD=3,由三角形面积公式可求
,求出BE长即可得到点E坐标. 由D是OB的中点可得OD=3,由三角形面积公式可求![]() .
.
(2)分两种情况,①点![]() 在
在![]() 上,②点
上,②点![]() 在
在![]() 上,设P点坐标为(x,y),根据三角形面积求法用x、y表示已知三角形面积即可.
上,设P点坐标为(x,y),根据三角形面积求法用x、y表示已知三角形面积即可.
(3)同(2)求出![]() ,结合(2)可知PQ=z-y.由(2)得两种情况即可求出对应的x值,即可的出P点坐标.
,结合(2)可知PQ=z-y.由(2)得两种情况即可求出对应的x值,即可的出P点坐标.
解:(1)①∵四边形![]() 为边长为6的正方形,
为边长为6的正方形,
∴B点坐标为(6,0),C点坐标为(6,6),A点坐标为(0,6)
∵![]() =
=![]() =2,
=2,
∴BE=2,
∴E点坐标为![]() ;
;
②∵正方形![]() 的边长为6,点
的边长为6,点![]() 为
为![]() 的中点,,
的中点,,
∴![]() ,
,
∴![]() ;
;
(2)

①点![]() 在
在![]() 上,
上,
∴![]()
∴![]() ,
,
∴![]() ;
;
②点![]() 在
在![]() 上,
上,
∴![]() ,
,
∴![]()
∴![]() ,
,![]() ;
;
(3)点![]() 在
在![]() 上,
上,
∴![]()
∴![]() ,
,
∴![]() ,
,
①点![]() 在
在![]() 上,
上,
∴![]() ,
,
∴![]() ,
,![]() 点坐标为
点坐标为![]() ;
;
②点![]() 在
在![]() 上,
上,
∴![]() ,
,
∴![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
综上,![]() 点坐标为
点坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目