Question

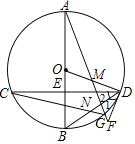
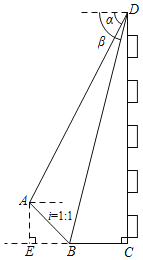
【题目】如图，已知二次函数的图象与x轴交于A、B两点，D为顶点，其中点B的坐标为，点D的坐标为．

（1）求该二次函数的表达式；

（2）点E是线段BD上的一点，过点E作x轴的垂线，垂足为F，且，求点E的坐标．

（3）试问在该二次函数图象上是否存在点G，使得的面积是的面积的？若存在，求出点G的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）点E的坐标为；（3）存在，点G的坐标为或.

【解析】

（1）依题意，利用二次函数的顶点式即可求

（2）可通过点B，点D求出线段BD所在的直线关系式，点E在线段BD上，即可设点E的坐标，利用点与点的关系公式，通过即可求

（3）先求线段AD所在的直线解析式，求利用点到直线的公式，即可求与的高，利用三角形面积公式即可求．

（1）依题意，设二次函数的解析式为

将点B代入得，得

∴二次函数的表达式为：

（2）依题意，点，点，设直线BD的解析式为

代入得，解得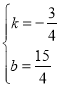

∴线段BD所在的直线为，

设点E的坐标为：

∴

∵

∴

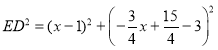
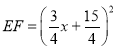
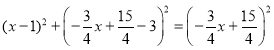
整理得

解得，（舍去）

故点E的纵坐标为

∴点E的坐标为

（3）存在点G，

设点G的坐标为

∵点B的坐标为，对称轴

∴点A的坐标为

∴设AD所在的直线解析式为

代入得，解得

∴直线AD的解析式为

∴ AD的距离为5

点G到AD的距离为：

由（2）知直线BD的解析式为：，

∵BD的距离为5

∴同理得点G至BD的距离为：

∴

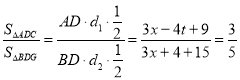
整理得

∵点G在二次函数上，

∴

代入得

整理得

解得，

此时点G的坐标为或