题目内容
18.如果等腰三角形的周长为10,一边长为3,那么这个等腰三角形的另两条边长为3和4或3.5和3.5.分析 题目给出等腰三角形一条边长为3,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解答 解:(1)当3是腰长时,底边为10-3×2=4,
此时4、3、3三边能够组成三角形,
所以另两边长为3,4;
(2)当3为底边长时,腰长为$\frac{1}{2}$×(10-3)=3.5,
此时3.5、3.5、3能够组成三角形,
所以另两边长为3.5,3.5.
所以另两边的长分别是3,4或3.5,3.5.
故答案为3,4或3.5,3.5.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
相关题目
8.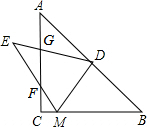 如图,已知点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.若△FCM的周长为16,则斜边AB的长为( )
如图,已知点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.若△FCM的周长为16,则斜边AB的长为( )
 如图,已知点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.若△FCM的周长为16,则斜边AB的长为( )
如图,已知点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.若△FCM的周长为16,则斜边AB的长为( )| A. | 4$\sqrt{2}$ | B. | 8$\sqrt{2}$ | C. | 16$\sqrt{2}$ | D. | 32$\sqrt{2}$ |
13.下列命题是假命题的是( )
| A. | 对角线互相垂直且相等的平行四边形是正方形 | |
| B. | 对角线互相垂直的矩形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 对角线互相垂直的四边形是正方形 |
3.下列运算正确的是( )
| A. | 3x2+2x3=5x6 | B. | (x3)2=x6 | C. | ${3}^{-2}=\frac{1}{6}$ | D. | 50=0 |
8.“打开电视,正在播广告”这一事件是( )
| A. | 必然事件 | B. | 确定事件 | C. | 不可能事件 | D. | 随机事件 |
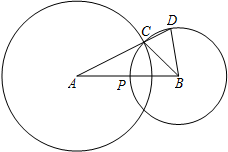 已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y.
已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y.