题目内容
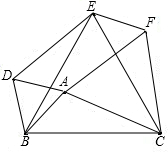 如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,当△ABC满足什么条件时,四边形ADEF是菱形?( )
如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,当△ABC满足什么条件时,四边形ADEF是菱形?( )| A、AB=AC |
| B、∠BAC=90° |
| C、∠BAC=120° |
| D、∠BAC=150° |
考点:菱形的判定
专题:
分析:根据等边三角形性质得出BD=AB,BE=BC,∠DBA=∠EBC=60°,求出∠DBE,证△DBE≌△ABC,推出DE=AC=AF,同理AD=EF得出平行四边形ADEF,根据菱形的判定判断即可.
解答:解:∵△ABD和△BCE是等边三角形,
∴BD=AB,BE=BC,∠DBA=∠EBC=60°,
∴∠DBE=∠CBA=60°-∠EBA,
在△DBE和△ABC中,
,
∴△DBE≌△ABC(SAS),
∴DE=AC,
∵△AFC是等边三角形,
∴AF=AC,
∴AF=DE,
同理AD=EF,
∴四边形ADEF是平行四边形,
当AB=AC时,∵AD=AB,AC=AF,
∴AD=AF,
∴四边形ADEF是菱形,
故选A.
∴BD=AB,BE=BC,∠DBA=∠EBC=60°,
∴∠DBE=∠CBA=60°-∠EBA,
在△DBE和△ABC中,
|
∴△DBE≌△ABC(SAS),
∴DE=AC,
∵△AFC是等边三角形,
∴AF=AC,
∴AF=DE,
同理AD=EF,
∴四边形ADEF是平行四边形,
当AB=AC时,∵AD=AB,AC=AF,
∴AD=AF,
∴四边形ADEF是菱形,
故选A.
点评:本题考查了平行四边形的性质和判定,菱形的判定的应用,注意:菱形的判定定理有:①有一组邻边相等的平行四边形是菱形,②四条边都相等的四边形是菱形,③对角线互相垂直的平行四边形是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲、乙、丙、丁四位同学同时参加一次数学竞赛,赛后他们四个预测获奖名次的谈话如下:
甲:丙第一,我第三名; 乙说:我第一名,丁第四名.
丙说:丁第二名,我第三名; 丁没有说话.
最后公布结果时,发现他们的预测都只猜对了一半,请你判定这四人的名次依次是( )
甲:丙第一,我第三名; 乙说:我第一名,丁第四名.
丙说:丁第二名,我第三名; 丁没有说话.
最后公布结果时,发现他们的预测都只猜对了一半,请你判定这四人的名次依次是( )
| A、甲、乙、丙、丁 |
| B、乙、甲、丙、丁 |
| C、乙、丙、丁、甲 |
| D、乙、丁、甲、丙 |
1克大米约50粒,如果每人每天浪费1粒大米,那么全国13亿人每天就要浪费大米约( )
| A、26千克 |
| B、2.6×102千克 |
| C、2.6×103千克 |
| D、2.6×104千克 |
 如图,已知点P是∠AOB的角平分线上的一点,且PC⊥OA,垂足为C,如果PC=4,那么点P到射线OB的距离是
如图,已知点P是∠AOB的角平分线上的一点,且PC⊥OA,垂足为C,如果PC=4,那么点P到射线OB的距离是