题目内容
12. 如图,设AD,BE,CF为三角形的三条高,若AB=6,BC=5,EF=3,则线段BE的长为$\frac{4}{5}$.
如图,设AD,BE,CF为三角形的三条高,若AB=6,BC=5,EF=3,则线段BE的长为$\frac{4}{5}$.
分析 根据AD,BE,CF为三角形的三条高,可得B,C,E,F四点共圆,证得△AEF∽△ABC,最后根据相似三角形的性质,代入数值进行求解.
解答 解:∵AD,BE,CF为△ABC的三条高,
∴B,C,E,F四点共圆,
∴△AEF∽△ABC,
∴$\frac{AF}{AC}$=$\frac{EF}{BC}$=$\frac{3}{5}$,
即cos∠BAC=$\frac{AF}{AC}$=$\frac{3}{5}$,
∴sin∠BAC=$\sqrt{1-(\frac{3}{5})^{2}}$=$\frac{4}{5}$,
∴在Rt△ABE中,
BE=ABsin∠BAC=6×$\frac{4}{5}$=$\frac{24}{5}$.
故答案为:$\frac{24}{5}$.
点评 本题考查了相似三角形的判定与性质,解答本题的关键是掌握相似三角形的判定与性质以及三角函数的知识.

练习册系列答案
相关题目
10.下列事件中,必然事件是( )
| A. | 掷一枚硬币,正面朝上 | |
| B. | 任意三条线段可以组成一个三角形 | |
| C. | 投掷一枚质地均匀的骰子,掷得的点数是奇数 | |
| D. | 抛出的篮球会下落 |
3.若a+b=0,则方程ax+b=0的解有( )
| A. | 只有一个解 | B. | 只有一个解或无解 | ||
| C. | 只有一个解或无数个解 | D. | 无解 |
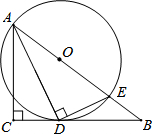 如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O
如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O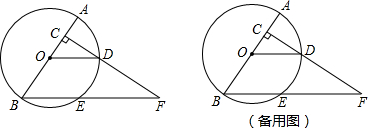
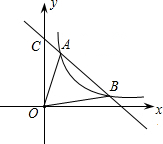 如图,一次函数y=-x+8和反比例函数y=$\frac{k}{x}$的图象在第一象限内有两个不同的公共点A(x1,y1)、B(x2,y2).
如图,一次函数y=-x+8和反比例函数y=$\frac{k}{x}$的图象在第一象限内有两个不同的公共点A(x1,y1)、B(x2,y2).