题目内容
19．
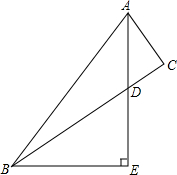如图，在△ABC中，AB=3AC，∠BAC的平分线交BC于点D，过点B作BE⊥AD，垂足为E，求证：AD=DE．
分析 延长AC、BE交于F，取CF的中点G，连结EG，首先根据ASA证明△ABE≌△AFE，则AB=AF，BE=FE，再根据AB=3AC，易知AC=CG=FG，根据平行线等分线段定理和逆定理可证明结论．
解答 证明：如图，延长AC、BE交于F，取CF的中点G，连结EG，
在△ABE和△AFE中，
$\left\{\begin{array}{l}{∠BAE=∠FAE}\\{AE=AE}\\{∠BEA=∠FEA=90°}\end{array}\right.$，
∴△ABE≌△AFE（ASA），
∴AB=AF，BE=FE，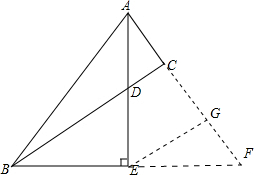
又∵AB=3AC，
∴AF=3AC，
∴CF=2AC，
又∵CG=FG，
∴AC=CG=FG
在△BCF中，
∵CG=FG，BE=FE，
∴EG∥BC，
又∵AC=CG，
∴AD=DE．
点评 本题主要考查了全等三角形的判定与性质以及平行线等分线段定理和逆定理，证明EG∥BC是解决问题的关键．
练习册系列答案
相关题目
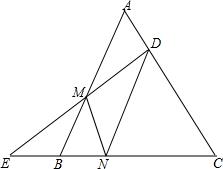如图已知在等边△ABC中，点D为边AC上一点，点E在CB的延长线上，且AD=BE，连接DE交边AB于点M，点N在BC上，且S△BEM=$\frac{1}{2}$S△NEM，求证：
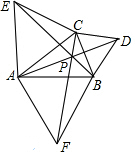如图，已知△ABC，分别以AC，BC，AB为边，作等边三角形ACE，BCD和ABF，连接AD，BE和CF交于点P，求证：PB+PC+PA=BE．
如图，△ABC的外角∠ACD的平分线CP的内角∠ABC平分线BP交于点P，且∠BAC=80°，求∠CAP．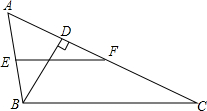
已知如图：在ABC中，BD⊥AC，E为AB的中点，EF∥BC，∠A=2∠C，求证：DF=$\frac{1}{2}$AB．
已知有三个数集：A={-1，3.1，-4，6，2.1}，B={-4.2，2.1，-1，10，-$\frac{1}{8}$}，C={21，-4.2，8，6}