题目内容
若关于x的一元二次方程kx2-2x+1=0有两个不相等的实数根,则实数k的取值范围是( )
| A、k>1 |
| B、k<1 |
| C、k>1且k≠0 |
| D、k<1且k≠0 |
考点:根的判别式,一元二次方程的定义
专题:
分析:根据一元二次方程的定义和△的意义得到k≠0且△>0,即(-2)2-4×k×1>0,然后解不等式即可得到k的取值范围.
解答:解:∵关于x的一元二次方程kx2-2x+1=0有两个不相等的实数根,
∴k≠0且△>0,即(-2)2-4×k×1>0,
解得k<1且k≠0.
∴k的取值范围为k<1且k≠0.
故选D.
∴k≠0且△>0,即(-2)2-4×k×1>0,
解得k<1且k≠0.
∴k的取值范围为k<1且k≠0.
故选D.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,∠AOB=90°,一动点P从O沿O→T→S折线运动,其中0°≤∠AOT≤90°,ST∥OA,且OT=4,ST=2,⊙I为△OST的内切圆,则⊙I的半径的最大值为( )
如图,∠AOB=90°,一动点P从O沿O→T→S折线运动,其中0°≤∠AOT≤90°,ST∥OA,且OT=4,ST=2,⊙I为△OST的内切圆,则⊙I的半径的最大值为( )A、3-
| ||
B、3+
| ||
| C、1 | ||
D、
|
小玲与小丽两人各掷一个正方体骰子,规定两人掷的点数和为偶数,则小玲胜;点数和为奇数,则小丽胜,下列说法正确的是( )
| A、此规则有利于小玲 |
| B、此规则有利于小丽 |
| C、此规则对两人是公平的 |
| D、无法判断 |
下列说法中,正确的有( )
①有一个角为60°的等腰三角形是等边三角形;
②三边长分别是1,
,3的三角形是直角三角形;
③一边上的中线等于这条边的一半的三角形是直角三角形;
④三个角之比为3:4:5的三角形是直角三角形.
①有一个角为60°的等腰三角形是等边三角形;
②三边长分别是1,
| 2 |
| 5 |
③一边上的中线等于这条边的一半的三角形是直角三角形;
④三个角之比为3:4:5的三角形是直角三角形.
| A、1个 | B、2个 | C、3个 | D、4个 |
下列说法中,正确的是( )
| A、分式的值一定是分数 |
| B、分母不为0,分式有意义 |
| C、分式的值为0,分式无意义 |
| D、分子为0,分式的值为0 |
下列式子中一定成立的是( )
| A、(x+2y)2=x2+4y2 |
| B、(x+5)(x-2)=x2-10 |
| C、(-x+y)2=(x-y)2 |
| D、(x+2y)(x-2y)=x2-2y2 |
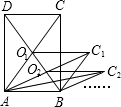 如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )
如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( ) 如图,已知抛物线y=ax2+4ax+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上.
如图,已知抛物线y=ax2+4ax+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上.