题目内容
(12分)(1)问题背景:如图1, 中,
中, ,
, ,
, 的平分线交直线
的平分线交直线 于
于 ,过点
,过点 作
作 ,交直线
,交直线 于
于 .请探究线段
.请探究线段 与
与 的数量关系.(事实上,我们可以延长
的数量关系.(事实上,我们可以延长 与直线
与直线 相交,通过三角形的全等等知识解决问题.)
相交,通过三角形的全等等知识解决问题.)
结论:线段 与
与 的数量关系是 ______ (请直接写出结论);
的数量关系是 ______ (请直接写出结论);
(2)类比探索:在(1)中,如果把 改为
改为 的外角
的外角 的平分线,其他条件均不变(如图2),(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由;
的平分线,其他条件均不变(如图2),(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由;
(3)拓展延伸:在(2)中,如果 ,且
,且 (
( ),其他条件均不变(如图3),请你直接写出
),其他条件均不变(如图3),请你直接写出 与
与 的数量关系.结论:
的数量关系.结论: _________
_________  (用含
(用含 的代数式表示).
的代数式表示).

(1) ;(2)仍然成立,证明过程略;(3)
;(2)仍然成立,证明过程略;(3)
【解析】
试题分析:(1)如图,分别延长 、
、 ,交于
,交于 .根据角平分线
.根据角平分线 和垂直关系
和垂直关系 ,由等腰三角形三线合一可得
,由等腰三角形三线合一可得  .(也可通过证明三角形全等)又根据
.(也可通过证明三角形全等)又根据 、两个直角以及
、两个直角以及 ,可证得
,可证得 ≌
≌ ,进而有
,进而有 ,所以
,所以 ;(2)思路同(1),仍然通过两次证明三角形全等得到线段关系,第一次全等;(3)思路依然同(1),延长两线段交于一点后先证明
;(2)思路同(1),仍然通过两次证明三角形全等得到线段关系,第一次全等;(3)思路依然同(1),延长两线段交于一点后先证明 ≌
≌ ,得到
,得到 ,再证明
,再证明 ∽
∽ ,且
,且
 ,所以有
,所以有 .
.

试题解析:(1) ;
;
(2)仍然成立,证明过程如下:分别延长 、
、 交于
交于 ,
, 平分
平分
 平分
平分







 ≌
≌

 ;
;
(3)
考点:(1)平面几何添加辅助线;(2)三角形全等的判定和性质;(3)三角形相似的判定和性质.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

 与y=kx+3的图像大致是( )
与y=kx+3的图像大致是( )
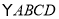 中,
中,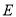 是
是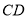 的延长线上一点,
的延长线上一点,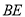 与
与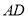 交于点
交于点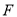 ,
,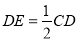 .
. 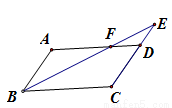
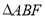 ∽
∽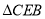 ;
;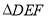 面积为2,求
面积为2,求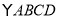 的面积.
的面积. 中,
中, ,
, 为
为 延长线上一点,
延长线上一点, 为
为 延长线上一点,
延长线上一点, ,当
,当 °时,
°时, ∽
∽ .
.
