题目内容
13.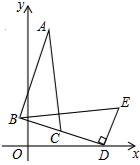 如图,在△BDE中,∠BDE=90°,BD=$6\sqrt{2}$,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为(4,3$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=$6\sqrt{2}$,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为(4,3$\sqrt{3}$).
分析 根据旋转的性质,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x轴于F,再根据点C在BD上确定出∠PDB=45°并求出PD的长,然后求出∠PDO=60°,根据直角三角形两锐角互余求出∠DPF=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得DF=$\frac{1}{2}$PD,利用勾股定理列式求出PF,再求出OF,即可得到点P,即旋转中心的坐标.
解答 解:如图,AB与BD的垂直平分线的交点即为旋转中心P,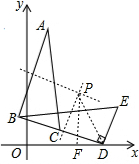
连接PD,过P作PF⊥x轴于F,
∵点C在BD上,
∴点P到AB、BD的距离相等,都是$\frac{1}{2}$BD,即$\frac{1}{2}$×6$\sqrt{2}$=3$\sqrt{2}$,
∴∠PDB=45°,
PD=3$\sqrt{2}$×$\sqrt{2}$=6,
∵∠BDO=15°,
∴∠PDO=45°+15°=60°,
∴∠DPF=30°,
∴DF=$\frac{1}{2}$PD=$\frac{1}{2}$×6=3,
∵点D的坐标是(7,0),
∴OF=OD-DF=7-3=4,
由勾股定理得,PF=$\sqrt{P{D}^{2}-D{F}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
即P点的坐标为(4,3$\sqrt{3}$),
故答案为:(4,3$\sqrt{3}$).
点评 本题考查了坐标与图形变化-旋转,熟练掌握旋转的性质确定出旋转中心的位置并得到含有30°角的直角三角形是解题的关键.

练习册系列答案
相关题目
4.平行四边形ABCD对角线交于点O,下列式子一定成立的是( )
| A. | AC⊥BD | B. | OA=OC | C. | AC=BD | D. | AO=OD |
1.下列计算正确的是( )
| A. | $\sqrt{9}=±3$ | B. | $-\sqrt{9}=-3$ | C. | |-3|=-3 | D. | -32=9 |
8.已知(x1,y1)(x2,y2)(x3,y3)是反比例函数y=-$\frac{4}{x}$的图象上的三个点,且x1<x2<0<x3,则y1、y2、y3的大小关系是y2>y1>y3(用“>”表示).
2.等腰三角形的一个角是50°,则它的底角是( )
| A. | 50° | B. | 50°或65° | C. | 80°或50° | D. | 65° |
 用一个平行于底面的平面去截如图放置的一个圆锥,将其分成上下两个几何体,如果设上面的小圆锥体积为x,下面的圆台体积为y,当截面由顶点向下平移时,y与x满足的函数关系的图象是( )
用一个平行于底面的平面去截如图放置的一个圆锥,将其分成上下两个几何体,如果设上面的小圆锥体积为x,下面的圆台体积为y,当截面由顶点向下平移时,y与x满足的函数关系的图象是( )


