题目内容
9.已知抛物线y=x2-2x-3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | 2 |
分析 设点A在点B的左侧,过点C作CD⊥AB于点D,将y=0代入y=x2-2x-3中即可求出点A、B的坐标,再利用配方法将抛物线的解析式由一般式变形为顶点式,由此即可得出点C的坐标,结合正切的定义即可得出tan∠CAB的值.
解答 解:设点A在点B的左侧,过点C作CD⊥AB于点D,如图所示.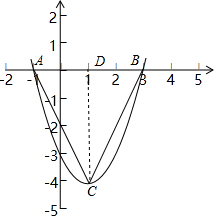
令y=x2-2x-3=(x+1)(x-3)=0,
解得:x1=-1,x2=3,
∴点A(-1,0),点B(3,0).
∵y=x2-2x-3=(x-1)2-4,
∴点C(1,-4),
∴点D(1,0).
∵AD=1-(-1)=2,CD=0-(-4)=4,
∴tan∠CAB=$\frac{CD}{AD}$=$\frac{4}{2}$=2.
故选D.
点评 本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征、正切的定义以及二次函数的三种形式,根据二次函数图象上点的坐标特征以及二次函数的性质找出点A、B、C的坐标是解题的关键.

练习册系列答案
相关题目
4. 如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )
 如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )| A. | 57° | B. | 66° | C. | 67° | D. | 44° |
1.下列计算正确的是( )
| A. | (a2)3=a5 | B. | a2+a3=a5 | C. | a2•a3=a5 | D. | a5÷a5=0 |
19.若点A(-3,y1),B(2,y2),C(3,y3)是函数y=-x+2图象上的点,则( )
| A. | y2<y3<y1 | B. | y1<y2<y3 | C. | y1<y3<y2 | D. | y1>y2>y3 |
 如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为8.
如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为8.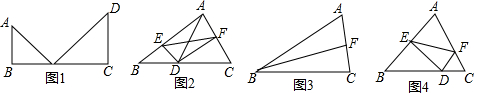
 如图,是某圆锥工件的三视图,则此工件的表面积为24πcm2.
如图,是某圆锥工件的三视图,则此工件的表面积为24πcm2.