Question

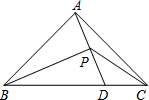如图，在三角形ABC中，BC＞BA，在BC上截取BD=BA，作∠ABC的平分线与AD相交于点P，连结PC，若△ABC的面积为4cm²，则△BPC的面积为（　　）

• A、0.5cm²
• B、1cm²
• C、1.5cm²
• D、2cm²

Answer 1

考点：等腰三角形的性质,三角形的面积

专题：

分析：根据等腰三角形三线合一的性质可得AP=PD，然后根据等底等高的三角形面积相等求出△BPC的面积等于△ABC面积的一半，代入数据计算即可得解．

解答：解：∵BD=BA，BP是∠ABC的平分线，
∴AP=PD，
∴S_△BPD=

1

2

S_△ABD，S_△CPD=

1

2

S_△ACD，
∴S_△BPC=S_△BPD+S_△CPD=

1

2

S_△ABD+

1

2

S_△ACD=

1

2

S_△ABC，
∵△ABC的面积为4cm²，
∴S_△BPC=

1

2

×4=2cm²．
故选：D．

点评：本题考查了等腰三角形三线合一的性质，三角形的面积，利用等底等高的三角形的面积相等求出△BPC的面积与△ABC的面积的关系是解题的关键．