Question

如图，△OPQ是边长为2的等边三角形，若正比例函数的图象过点P，则它的解析式是________．

Answer 1

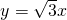
分析：过点P作PD⊥x轴于点D，由等边三角形的性质可知OD=OQ=1，再根据勾股定理求出PD的长，故可得出P点坐标，再利用待定系数法求出直线OP的解析式即可．
解答：解：过点P作PD⊥x轴于点D，
∵△OPQ是边长为2的等边三角形，
∴OD=OQ=×2=1，
在Rt△OPD中，
∵OP=2，OD=1，
∴PD===，
∴P（1，），
设直线OP的解析式为y=kx（k≠0），
∴=k，
∴直线OP的解析式为y=x．
故答案为：y=x．
点评：本题考查的是用待定系数法求正比例函数的解析式，先根据题意得出点P的坐标是解答此题的关键．