题目内容
13.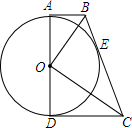 如图,在直角梯形ABCD中,AB∥CD,以AD为直径的圆切BC于E,连接OB、OC,试探究OB与OC有何位置关系?
如图,在直角梯形ABCD中,AB∥CD,以AD为直径的圆切BC于E,连接OB、OC,试探究OB与OC有何位置关系?
分析 连结OE,由切线的性质得OE⊥BC,再利用直角梯形的定义得到AD⊥AB,AD⊥CD,则可判断AB和CD都是⊙O的切线,根据切线长定理得到BA=BE,CE=CD,于是根据角平分线性质定理的逆定理得到OB平分∠AOE,OC平分∠DOE,则∠1+∠2=$\frac{1}{2}$(∠AOE+∠DOE)=90°,即∠BOC=90°,所以OB⊥OC.
解答 解:OB与OC垂直.理由如下:
连结OE,
∵以AD为直径的圆切BC于E,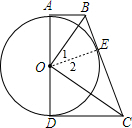
∴OE⊥BC,
∵四边形ABCD为直角梯形,AB∥CD,
∴∠BAD=∠CDA=90°,
∴AD⊥AB,AD⊥CD,
而AD为直径,
∴AB和CD都是⊙O的切线,
∴BA=BE,CE=CD,
∴OB平分∠AOE,OC平分∠DOE,
∴∠1=$\frac{1}{2}$∠AOE,∠2=$\frac{1}{2}$∠DOE,
∴∠1+∠2=$\frac{1}{2}$(∠AOE+∠DOE)=$\frac{1}{2}$×180°=90°,即∠BOC=90°,
∴OB⊥OC.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了直角梯形和角平分线的性质定理的逆定理.

练习册系列答案
相关题目
2.某文具盒每周的销量与售价的相关信息如下表:
已知该文具盒的进价为6元/个,设售价为x元/个,每周销量为y个.
(1)请直接写出y与x的函数关系式;
(2)设每周的销售利润为W元,求出W与x的函数关系式;
(3)若要使该文具盒的每周利润达到96元,且销量更大,销售单位应定为多少元?
| 售价(元/个) | 10 | 11 | 12 | 13 | … |
| 每周销量(个) | 20 | 18 | 16 | 14 | … |
(1)请直接写出y与x的函数关系式;
(2)设每周的销售利润为W元,求出W与x的函数关系式;
(3)若要使该文具盒的每周利润达到96元,且销量更大,销售单位应定为多少元?
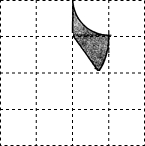 如图,已知网格中每个小正方形的边长都是1,图中的图案由两段以格点为圆心,分别以1和2为半径的圆弧和网格的边围成.
如图,已知网格中每个小正方形的边长都是1,图中的图案由两段以格点为圆心,分别以1和2为半径的圆弧和网格的边围成.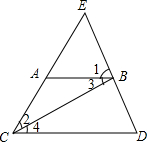 如图,下列推理所注的依据正确的是(3)(填序号)
如图,下列推理所注的依据正确的是(3)(填序号)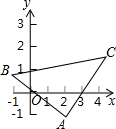 如图,直角坐标系中A(2,-1),B(-1,1),∠BAC=90°,AB=AC,求C点坐标.
如图,直角坐标系中A(2,-1),B(-1,1),∠BAC=90°,AB=AC,求C点坐标.