题目内容
在△ABC中,AB=15cm,BC=20cm,AC=30cm,另一个与它相似的△A′B′C′的最短边长为45cm,则△A′B′C′的周长为
195cm .
考点: 相似三角形的性质.
分析: 利用最短边可求得两三角形的相似比,且可求得△ABC的周长,再根据周长比等于相似比可求得△A′B′C′的周长.
解答: 解:
∵△ABC∽△A′B′C′,且△ABC中最短边为15cm,△A′B′C′的最短边长为45cm,
∴相似比为 =
= ,
,
∴ =
= ,
,
又△ABC的周长为15+20+30=65(cm),
∴ =
= ,
,
解得C△A′B′C′=195cm,
故答案为:195cm.
点评: 本题主要考查相似三角形的性质,掌握相似三角形的周长比等于相似比是解题的关键.

练习册系列答案
相关题目
 处,则AP的长为__________.
处,则AP的长为__________.
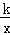 (x>0)上,则k的值为( )
(x>0)上,则k的值为( )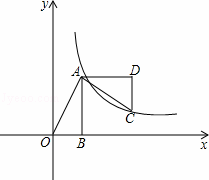
 的图象(请画图)回答问题:当函数值为正时,x的取值范围是
的图象(请画图)回答问题:当函数值为正时,x的取值范围是 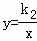 (x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.
(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.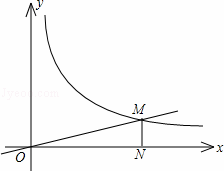
 =
=  +|7|+(
+|7|+( )0+(
)0+( )﹣1.
)﹣1.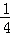 B.
B. 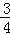 C.
C.  D. 1
D. 1