Question

如图，平面直角坐标系中，OB在x轴上，∠ABO=90°，点A的坐标为（1，2），将△AOB绕点A逆时针旋转90°，点O的对应点C恰好落在双曲线y=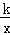（x＞0）上，则k的值为（　　）

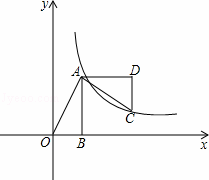
　 A． 2 B． 3 C． 4 D． 6

Answer 1

B

考点： 反比例函数图象上点的坐标特征；坐标与图形变化-旋转． 

分析： 由旋转可得点D的坐标为（3，2），那么可得到点C的坐标为（3，1），那么k等于点C的横纵坐标的积．

解答： 解：易得OB=1，AB=2，

∴AD=2，

∴点D的坐标为（3，2），

∴点C的坐标为（3，1），

∴k=3×1=3．

故选：B．

点评： 解决本题的关键是利用旋转的性质得到在反比例函数上的点C的坐标．