Question

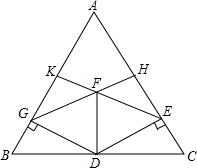已知△ABC中，AB=AC，点D是BC中点，DE⊥AC于点E，DG⊥AB于G，EK⊥AB于K，GH⊥AC于H，EK和GH相交于F，求证：四边形DEFG是菱形．

Answer 1

考点：菱形的判定

专题：证明题

分析：先求出四边形是平行四边形，证三角形全等，得出DG=DE，根据菱形的判定得出即可．

解答：证明：∵DE⊥AC，DG⊥AB，EK⊥AB，GH⊥AC，
∴∠DGB=∠DEC=90°，EK∥DG，DE∥GH，
∴四边形DEFG是平行四边形，
∵AB=AC，
∴∠B=∠C，
在△DGB和△DEC中，

∠B=∠C ∠DGB=∠DEC BD=DC

，
∴△DGB≌△DEC（AAS），
∴DG=DE，
∵四边形DEFG是平行四边形，
∴四边形DEFG是菱形．

点评：本题考查了全等三角形的性质和判定，菱形的判定，平行四边形的判定的应用，主要考查学生的推理能力，注意：有一组邻边相等的平行四边形是菱形．