题目内容
已知：如图，在半径为4的⊙O中，AB为直径，以弦
（非直径）为对称轴将
折叠后与
相交于点
，如果
，那么的长为
A．
B．
C．
D．
【答案】
A.
【解析】
试题分析：如图，AC为折叠线，把折叠线看作对称轴，折叠后得到的弧AC所在的⊙P与⊙O关于AC对称，如图，连接DF,CF,BC,根据直径所对的圆周角是直角，可知:点B、C、F三点共线，即△ABF是等腰三角形，且AC⊥BF，FD⊥AB，由AO=4，AD=3DB可得：AD=6，BD=2，AB=8，由轴对称可知：AF=8，所以
，
；根据
可以求出
,故选A.
考点：1、轴对称的性质；2、圆周角定理；3、勾股定理.
练习册系列答案
应用题作业本系列答案
相关题目
于点E，且EM＞MC．连接DE，DE=
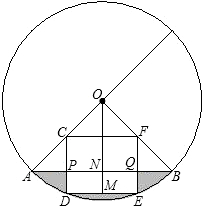已知：如图，在半径为4的⊙O中，圆心角∠AOB=90°，以半径OA、OB的中点C、F为顶点作矩形CDEF，顶点D、E在⊙O的劣弧
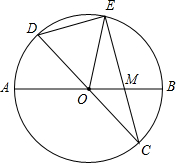
上滑动并保持AE=CF，但点F不与A、C重合，点E不与A、B重合．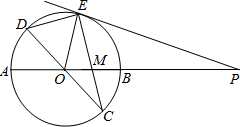
已知：如图，在半径为4的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE=
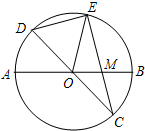已知：如图，在半径为8的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE=