题目内容
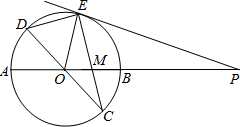 已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=| 15 |
(1)求证:AM•MB=EM•MC;
(2)求sin∠EOB的值;
(3)若P是直径AB延长线上的点,且BP=12,求证:直线PE是⊙O的切线.
分析:(1)连接AE,BC,由同弧所对的圆周角相等得到一对角相等,再根据对顶角相等,利用两对应角相等的两三角形相似,得到三角形AEM与三角形CBM相似,由相似得比例,化简后即可得证;
(2)根据圆周角定理及勾股定理可求出CE的长,再由相交弦定理求出EM的长,根据所求EM的长与半径相等判断出△OEM为等腰三角形,过E作EF⊥OM,根据等腰三角形的性质及勾股定理可求出OF,EF的长,进而求出sin∠EOB的值;
(3)由EO=EM,EF垂直于OM,得到F为OM的中点,由M为OB中点,求出OM的长,可得出OF的长,由OB+BP=OP,得出OP的长,利用OP-OF求出FP的长,再由EF的长,利用勾股定理求出EP的长,在三角形OEP中,再利用勾股定理的逆定理判断出三角形OEP为直角三角形,可得∠OEP为直角,即EP垂直于OE,可得EP为圆O的切线.
(2)根据圆周角定理及勾股定理可求出CE的长,再由相交弦定理求出EM的长,根据所求EM的长与半径相等判断出△OEM为等腰三角形,过E作EF⊥OM,根据等腰三角形的性质及勾股定理可求出OF,EF的长,进而求出sin∠EOB的值;
(3)由EO=EM,EF垂直于OM,得到F为OM的中点,由M为OB中点,求出OM的长,可得出OF的长,由OB+BP=OP,得出OP的长,利用OP-OF求出FP的长,再由EF的长,利用勾股定理求出EP的长,在三角形OEP中,再利用勾股定理的逆定理判断出三角形OEP为直角三角形,可得∠OEP为直角,即EP垂直于OE,可得EP为圆O的切线.
解答: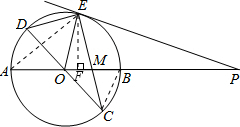
解:(1)连接AE,BC,
∵∠AEC与∠MBC都为
所对的圆周角,
∴∠AEC=∠MBC,又∠AME=∠BMC(对顶角相等),
∴△AME∽△CMB,
∴AM:CM=EM:MB,即AM•MB=EM•MC;
(2)如图,∵DC为⊙O的直径,
∴DE⊥EC,
∵DC=8,DE=
,
∴EC=
=
=7,
设EM=x,由于M为OB的中点,
∴BM=2,AM=6,
∴AM•MB=x•(7-x),即6×2=x(7-x),
整理得:x2-7x+12=0,
解得:x1=3,x2=4,
∵EM>MC,∴EM=4,
∵OE=EM=4,
∴△OEM为等腰三角形,
过E作EF⊥OM,垂足为F,则OF=
OM=1,
∴EF=
=
=
,
∴sin∠EOB=
;
(3)在Rt△EFP中,EF=
,PF=FB+BP=3+12=15,
根据勾股定理得:EP=
=
=4
,
又OE=4,OP=OB+BP=4+12=16,
∴OE2+EP2=16+240=256,OP2=256,
∴OE2+EP2=OP2,
∴∠OEP=90°,
则EP为圆O的切线.

解:(1)连接AE,BC,
∵∠AEC与∠MBC都为
 |
| AC |
∴∠AEC=∠MBC,又∠AME=∠BMC(对顶角相等),
∴△AME∽△CMB,
∴AM:CM=EM:MB,即AM•MB=EM•MC;
(2)如图,∵DC为⊙O的直径,
∴DE⊥EC,
∵DC=8,DE=
| 15 |
∴EC=
| DC2-DE2 |
| 64-15 |
设EM=x,由于M为OB的中点,
∴BM=2,AM=6,
∴AM•MB=x•(7-x),即6×2=x(7-x),
整理得:x2-7x+12=0,
解得:x1=3,x2=4,
∵EM>MC,∴EM=4,
∵OE=EM=4,
∴△OEM为等腰三角形,
过E作EF⊥OM,垂足为F,则OF=
| 1 |
| 2 |
∴EF=
| OE2-OF2 |
| 16-1 |
| 15 |
∴sin∠EOB=
| ||
| 4 |
(3)在Rt△EFP中,EF=
| 15 |
根据勾股定理得:EP=
| EF2+FP2 |
| 240 |
| 15 |
又OE=4,OP=OB+BP=4+12=16,
∴OE2+EP2=16+240=256,OP2=256,
∴OE2+EP2=OP2,
∴∠OEP=90°,
则EP为圆O的切线.
点评:此题考查了切线的判定,相似三角形的判定与性质,勾股定理及逆定理,圆周角定理,等腰三角形的判定与性质,以及锐角三角函数定义,其中证明切线的方法有两种:有点连接此点与圆心证直线与半径垂直;无点作垂线证明垂线段等于半径.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
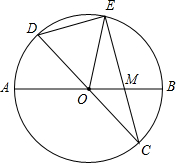 于点E,且EM>MC.连接DE,DE=
于点E,且EM>MC.连接DE,DE=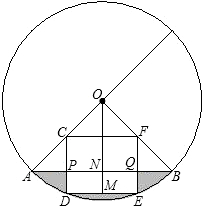 已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧
已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧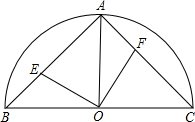 上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.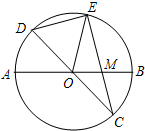 已知:如图,在半径为8的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为8的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=