题目内容
13．
如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（1，3），点M是坐标轴上的一点，使△AOM为等腰三角形的点M的个数有（ ）| A． | 5 个 | B． | 6 个 | C． | 7 个 | D． | 8个 |
分析 分别以O、A为圆心，以OA长为半径作圆，与坐标轴交点即为所求点M，再作线段OA的垂直平分线，与坐标轴的交点也是所求的点M求解即可．
解答 解：①以A为圆心，以OA为半径画弧，交坐标轴分别有2个点，即2个点符合，
②以O为圆心，以OA为半径画弧，交坐标轴分别有4个点，即4个点符合，
③作AO的垂直平分线分别交坐标轴分别有2个点，即2个点符合，
2+4+2=8；
故选D
点评 此题主要考查了坐标与图形的性质及等腰三角形的判定；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．
练习册系列答案
名校课堂系列答案
相关题目
4．抛物线y=-（x-2）2+2的对称轴是（ ）
| A． | 直线x=1 | B． | 直线x=-1 | C． | 直线x=2 | D． | 直线x=-2 |
1．
如图，正方形ABCD内有两点E、F满足AE=1，EF=FC=3，AE⊥EF，CF⊥EF，则正方形ABCD的面积为（ ）
如图，正方形ABCD内有两点E、F满足AE=1，EF=FC=3，AE⊥EF，CF⊥EF，则正方形ABCD的面积为（ ）| A． | $\frac{25}{2}$ | B． | 10$\sqrt{2}$ | C． | 20 | D． | 20$\sqrt{2}$ |
如图，已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+m（k≠0）的图象相交于点A（-2，4），B（9，2），那么能使y2＞y1成立的x的取值范围是-2＜x＜9．
如图，已知点A（0，4）、点B（6，4），点C在x轴上，若△ABC是等腰三角形，则点C的横坐标为$6-2\sqrt{5}$或$6+2\sqrt{5}$或3或$-2\sqrt{5}$或$2\sqrt{5}$．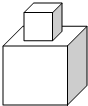
如图所示的某种玩具是由两个正方体用胶水黏合而成的，它们的棱长分别为1dm和2dm，为了美观，现要在其表面喷涂油漆，如果喷涂1dm2需用油漆4g，那么喷涂这个玩具共需油漆112g．