题目内容
若Rt△ABC中两条边长为6和8，则该三角形面积为________．
24或6
分析：由Rt△ABC中两条边长为6和8：①可知6和8为Rt△ABC的两条直角边，直接求的面积；②当8为Rt△ABC的斜边，6为一条直角边，利用勾股定理求得另一条直角边，再求面积．
解答：第一种情况：
当6和8为Rt△ABC的两条直角边时，
SRt△ABC=
×6×8=24；
第二种情况：
当8为Rt△ABC的斜边，6为一条直角边，根据勾股定理有，
另一条直角边=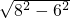
=2，
SRt△ABC=×6×2=6；
综上所知，三角形面积为24或6．
故填24或6．
点评：此题考查勾股定理与三角形的面积计算方法．
分析：由Rt△ABC中两条边长为6和8：①可知6和8为Rt△ABC的两条直角边，直接求的面积；②当8为Rt△ABC的斜边，6为一条直角边，利用勾股定理求得另一条直角边，再求面积．
解答：第一种情况：
当6和8为Rt△ABC的两条直角边时，
SRt△ABC=
×6×8=24；第二种情况：
当8为Rt△ABC的斜边，6为一条直角边，根据勾股定理有，
另一条直角边=
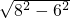=2，SRt△ABC=
×6×2=6；综上所知，三角形面积为24或6
．故填24或6
．点评：此题考查勾股定理与三角形的面积计算方法．
练习册系列答案
智慧小复习系列答案
相关题目
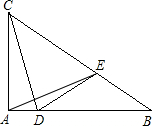点E沿BC从B向C运动，速度为2cm/秒．动点E到达点C时运动终止．连接DE、CD、AE．