题目内容
18. 如图⊙O,半径为3,弦AB=$3\sqrt{2}$,则弦AB所对的圆心角等于90°.
如图⊙O,半径为3,弦AB=$3\sqrt{2}$,则弦AB所对的圆心角等于90°.
分析 过点O作OD⊥AB于点D,根据垂径定理求出BD的长,由锐角三角函数的定义求出∠BOD的度数,进而可得出结论.
解答  解:过点O作OD⊥AB于点D,
解:过点O作OD⊥AB于点D,
∵AB=3$\sqrt{2}$,
∴BD=$\frac{3\sqrt{2}}{2}$,
∴sin∠BOD=$\frac{BD}{OB}$=$\frac{\frac{3\sqrt{2}}{2}}{3}$=$\frac{\sqrt{2}}{2}$,
∴∠BOD=45°,
∴∠AOB=2∠BOD=90°.
故答案为:90°.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.观察下列图形,通过折叠能围成一个正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
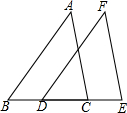 如图,在△ABC和△FDE中,若AB=FD,∠A=∠F,则只需增加条件AC=EF或者增加条件∠B=∠FDE,就可以证明△ABC≌△FDE.(每空只填一个即可)
如图,在△ABC和△FDE中,若AB=FD,∠A=∠F,则只需增加条件AC=EF或者增加条件∠B=∠FDE,就可以证明△ABC≌△FDE.(每空只填一个即可)
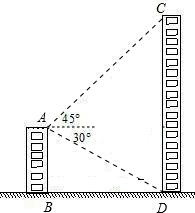 如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°,已知楼AB的高度为12米.求楼CD的高(结果保留根号).
如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°,已知楼AB的高度为12米.求楼CD的高(结果保留根号).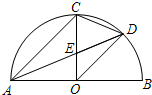 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连结CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④CD2=CE•CO.其中正确结论的序号是①④.
如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连结CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④CD2=CE•CO.其中正确结论的序号是①④. 如图,一个刷成黑白色且能折成长方体的模型,由它折成的长方体是下列图形中的哪一个( )
如图,一个刷成黑白色且能折成长方体的模型,由它折成的长方体是下列图形中的哪一个( )






