题目内容
 如图,⊙O是温州某公园的一个圆形雕塑,在某一时刻,太阳照射下它的影子AB的长为5m,此时,身高为1.5m的小芳的影长为2m,则这个圆形雕塑的半径为( )
如图,⊙O是温州某公园的一个圆形雕塑,在某一时刻,太阳照射下它的影子AB的长为5m,此时,身高为1.5m的小芳的影长为2m,则这个圆形雕塑的半径为( )分析:根据光学原理画出图形,利用相似三角形的性质及勾股定理计算即可.
解答: 解:如图:
解:如图:
连接EF,EB,根据光的直线传播及太阳的遥远程度可知BF∥AE,
∵EF⊥BF,EF⊥AE,
∴△EBF为直角三角形,
易得,△EBF∽△AEB---①.
∵
=
,
解得,EB=
,
∴AE=
=
,
由①可得,
=
,
即
=
,
解得,EF=3,
故半径为
×3=
.
故选D.
 解:如图:
解:如图:连接EF,EB,根据光的直线传播及太阳的遥远程度可知BF∥AE,
∵EF⊥BF,EF⊥AE,
∴△EBF为直角三角形,
易得,△EBF∽△AEB---①.
∵
| EB |
| 5 |
| 1.5 |
| 2 |
解得,EB=
| 15 |
| 4 |
∴AE=
52+(
|
| 25 |
| 4 |
由①可得,
| EF |
| AB |
| EB |
| AE |
即
| EF |
| 5 |
| ||
|
解得,EF=3,
故半径为
| 1 |
| 2 |
| 3 |
| 2 |
故选D.
点评:本题考查了相似三角形的应用,正确作出辅助线是解题的关键.

练习册系列答案
相关题目
 如图,AC是我市某大楼的高,在地面上B点处测得楼顶A的仰角为45°,沿BC方向前进18米到达D点,测得tan∠ADC=
如图,AC是我市某大楼的高,在地面上B点处测得楼顶A的仰角为45°,沿BC方向前进18米到达D点,测得tan∠ADC= 如图,⊙O是温州某公园的一个圆形雕塑,在某一时刻,太阳照射下它的影子AB的长为5m,此时,身高为1.5m的小芳的影长为2m,则这个圆形雕塑的半径为
如图,⊙O是温州某公园的一个圆形雕塑,在某一时刻,太阳照射下它的影子AB的长为5m,此时,身高为1.5m的小芳的影长为2m,则这个圆形雕塑的半径为


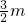
 .现打算从大楼顶端A点悬挂一幅庆祝建国60周年的大型标语,若标语底端距地面15m,请你计算标语AE的长度应为多少?
.现打算从大楼顶端A点悬挂一幅庆祝建国60周年的大型标语,若标语底端距地面15m,请你计算标语AE的长度应为多少?
 .现打算从大楼顶端A点悬挂一幅庆祝建国60周年的大型标语,若标语底端距地面15m,请你计算标语AE的长度应为多少?
.现打算从大楼顶端A点悬挂一幅庆祝建国60周年的大型标语,若标语底端距地面15m,请你计算标语AE的长度应为多少?