题目内容
直线y=-
x+2k与双曲线y=
，其中k＞0，交于B、C两点（其中B在点C的上方），直线与y轴的交点为A点，若AB+AC=
，则k的值是 ．
| 3 |
| ||
| x |
8
| ||
| 3 |
考点：反比例函数与一次函数的交点问题
专题：计算题
分析：直线y=-
x+2k与x轴交于D点，作BE⊥y轴于E点，CF⊥y轴于F点，先确定A（0，2k），D（
，0），再根据正切的定义可计算出∠OAD=30°，则AB=2BE，AC=2CF，
设B点坐标为（x1，y1），C点坐标为（x2，y2），然后解两函数解析式所组成的方程组得到关于x的一元二次方程
x2-2kx+
k=0，利用根与系数的关系得到x1+x2=
=
，根据AB+AC=
得到2×
k=
，最后解关于k的一次方程即可．
| 3 |
2
| ||
| 3 |
设B点坐标为（x1，y1），C点坐标为（x2，y2），然后解两函数解析式所组成的方程组得到关于x的一元二次方程
| 3 |
| 3 |
| 2k | ||
|
2
| ||
| 3 |
8
| ||
| 3 |
2
| ||
| 3 |
8
| ||
| 3 |
解答：解：如图，直线y=-
x+2k与x轴交于D点，作BE⊥y轴于E点，CF⊥y轴于F点，
∵A点坐标为（0，2k），D点坐标为（
，0），
∴tan∠OAD=
=
=
，
∴∠OAD=30°，
∴AB=2BE，AC=2CF，
设B点坐标为（x1，y1），C点坐标为（x2，y2），
解方程组
得
x2-2kx+
k=0，
∴x1+x2=
=
，
∵AB+AC=
，
∴2（BE+CF）=
，
∴2×
k=
，
∴k=2．
故答案为2．
| 3 |
∵A点坐标为（0，2k），D点坐标为（
2
| ||
| 3 |
∴tan∠OAD=
| OD |
| OA |
| ||||
| 2k |
| ||
| 3 |
∴∠OAD=30°，
∴AB=2BE，AC=2CF，
设B点坐标为（x1，y1），C点坐标为（x2，y2），
解方程组
|
| 3 |
| 3 |
∴x1+x2=
| 2k | ||
|
2
| ||
| 3 |
∵AB+AC=
8
| ||
| 3 |
∴2（BE+CF）=
8
| ||
| 3 |
∴2×
2
| ||
| 3 |
8
| ||
| 3 |
∴k=2．
故答案为2．
点评：本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数的交点坐标满足两个函数的解析式．也考查了特殊角三角形函数以及一元二次方程根与系数的关系．
练习册系列答案
优等生题库系列答案
相关题目
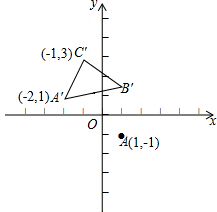在平面直角坐标系中，△ABC的顶点A的坐标为（1，-1），平移△ABC得到△A′B′C′（如图所示），平移后点A的对应点是A′（-2，1），点C的对应点是C′（-1，3），则平移前点C的坐标为由五个完全相同的小正方形组合而成的立体图形如图所示，它的正视图是（ ）
A、 |
B、 |
C、 |
D、 |
