��Ŀ����
10����֪����������y=$\frac{k}{x}$��ͼ����һ�κ���y=kx+m��ͼ���ཻ�ڵ�A��2��1������1���ֱ���������������Ľ���ʽ��
��2������������ֵ����0ʱ��x��ȡֵ��Χ��
��3����һ�κ����뷴������������һ������ΪB����������Ϊ-4����x��ȡֵ��ʲô��Χ��ʱ��������������ֵ����һ�κ�����ֵ����x��ȡֵ��ʲô��Χ��ʱ��������������ֵС��һ�κ�����ֵ��
���� ��1���Ȱ�A���������y=$\frac{k}{x}$�����k����A���������y=kx+m��Ȼ�����ô���ϵ������һ�κ�������ʽ��
��2�����ݷ��������������ʣ����x��ȡֵ��Χ���ɣ�
��3������������ͼ���ݺ���ͼ����������ͼ����һ�κ���ͼ���Ϸ�������������ͼ����һ�κ���ͼ���·��ó�x��ȡֵ��
��� �⣺��1���߷���������y=$\frac{k}{x}$��ͼ����һ�κ���y=kx+m��ͼ���ཻ�ڵ�A��2��1����
��k=2��m=-3��
�෴���������Ľ���ʽΪy=$\frac{2}{x}$��һ�κ����Ľ���ʽΪy=2x-3��
��2���߷����������Ľ���ʽΪy=$\frac{2}{x}$��
��ͼ��λ��һ�������ޣ�
�൱x��0ʱ��������������ֵ����0��
�����������ֵ����0ʱ��x��ȡֵ��Χ��x��0��
��3������������ͼ����ͼ��
��B���������Ϊ-4��
��-4=$\frac{2}{x}$�����x=-$\frac{1}{2}$��
��B��-$\frac{1}{2}$��-4����
��A��2��1����
����ͼ���֪����-$\frac{1}{2}$��x��0��x��2ʱ��������������ֵС��һ�κ�����ֵ��
���� ���⿼���˷�����������һ�κ����Ľ���ʽ�Ľ������⣬�ô���ϵ������������һ�κ����Ľ���ʽ�Լ������Ͳ���ʽ�Ĺ�ϵ�����ν��˼��������ǽ���Ĺؼ���

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д�| A�� | ��-2��3�� | B�� | ��-3��2�� | C�� | ��3��2�� | D�� | ��2��-3�� |
| A�� | -$\frac{11}{4}$ | B�� | 7 | C�� | 7��-$\frac{3}{7}$ | D�� | -$\frac{11}{4}$��-$\frac{9}{8}$ |
 ��֪һ�κ���y=x+2
��֪һ�κ���y=x+2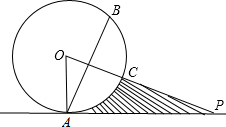 ��ͼ����P��ԲO�⣬PA��ԲO������C�㣬��B���A����ֱ��PO�Գƣ���֪OA=4����P=30�㣬��
��ͼ����P��ԲO�⣬PA��ԲO������C�㣬��B���A����ֱ��PO�Գƣ���֪OA=4����P=30�㣬�� ��ͼ��ƽ�����й����˵�İ�������0A��OB��OC��OD��OE��OF��OG��OH��������OA��ʼ����ʱ�뷽��������������д������1��2��3��4��5��6��7��8��
��ͼ��ƽ�����й����˵�İ�������0A��OB��OC��OD��OE��OF��OG��OH��������OA��ʼ����ʱ�뷽��������������д������1��2��3��4��5��6��7��8��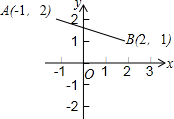 ��֪ƽ��ֱ������ϵ�У�A��-1��2����B��2��1�����߶�AB��y����C��
��֪ƽ��ֱ������ϵ�У�A��-1��2����B��2��1�����߶�AB��y����C�� ��ͼ���ڡ�ABC�У���A=40�㣬��һ��ֱ�����ǰ�DEF������ֱ�DZ�DE��DF�ֱ���B��C����ֱ�Ƕ���D���������ⲿ�����ABD+��ACD�Ķ�����230�ȣ�
��ͼ���ڡ�ABC�У���A=40�㣬��һ��ֱ�����ǰ�DEF������ֱ�DZ�DE��DF�ֱ���B��C����ֱ�Ƕ���D���������ⲿ�����ABD+��ACD�Ķ�����230�ȣ�