题目内容
已知| b |
| a |
| d |
| c |
| a+b |
| a-b |
| c+d |
| c-d |
分析：根据比例的合分比性质，对已知的比例等式变形即可证明．
解答：证明：设
=
=k，
∴b=ak，d=ck，
将其代入可得：
=
，
=
，
∴
=
．
| b |
| a |
| d |
| c |
∴b=ak，d=ck，
将其代入可得：
| a+b |
| a-b |
| k+1 |
| 1-k |
| c+d |
| c-d |
| k+1 |
| 1-k |
∴
| a+b |
| a-b |
| c+d |
| c-d |
点评：考查合分比性质．一个比例里，第一个前后项之和与它们的差的比，等于第二个比的前后项的和与它们的差的比．这叫做比例中的合分比定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知线段AB=3cm，延长AB到C，使BC=6 cm，又延长BA到D，使DA=1 cm，下列结论正确的是（ ）
A、DB=
| ||
B、DC=
| ||
C、DA=
| ||
D、DB=
|
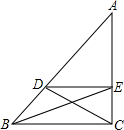如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，AD=2BD，已知