题目内容
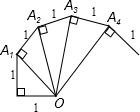
如图，细心观察图形，认真分析，然后回答下列问题：
（1）OA1=______，OA2=______，OA3=______，…，OAn=______；
（2）如果第一个三角形的面积用S1表示，其它依此类推．那么S1=______，S2=______，S3=______，…，Sn=______．
（3）求S21+S22+S23+…S2100的值．
解：（1）根据勾股定理求值：OA1=
=
；OA2=
=
，那么OA3=
；OAn=
；
（2）S1=
×1×1=；S2=×=
，同理可得S3=
，Sn=
；
（3）原式=
=
××（1+100）×100=
．
分析：（1）根据勾股定理直接计算即可；（2）根据具体数值推出规律解答；（3）展开后分母都为4，把分子相加即可．
点评：解决本题的关键是利用勾股定理求得相应的线段长，得到一定规律，并运用这一规律解决问题．
=；OA2==，那么OA3=；OAn=；（2）S1=
×1×1=；S2=×=，同理可得S3=，Sn=；（3）原式=
=××（1+100）×100=．分析：（1）根据勾股定理直接计算即可；（2）根据具体数值推出规律解答；（3）展开后分母都为4，把分子相加即可．
点评：解决本题的关键是利用勾股定理求得相应的线段长，得到一定规律，并运用这一规律解决问题．
练习册系列答案
新思维寒假作业系列答案
相关题目
)2＋1＝2，S1＝
；
)2＋1＝3，S2＝
)2＋1＝4，S3＝
，
；
，
；
，
