题目内容
如图,菱形ABCD中,AB=2,∠D=60°,菱形ABCD在直线上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作.
(1)对角线AC= ;
(2)经过27次这样的操作菱形中心O所经过的路径总长为(结果保留π) .
【答案】分析:(1)根据菱形四边相等的性质可得出△ABC是等边三角形,继而可得出AC的长度;
(2)从图中可以看出,第一次旋转是以点B为圆心,那么菱形中心旋转的半径就是OB,解直角三角形可求出OB的长,圆心角是60°,第二次还是以点B为圆心,那么菱形中心旋转的半径就是OB,圆心角是60°,第三次就是以点C为旋转中心,OC为半径,旋转的圆心角为60°,旋转到此菱形就又回到了原图,故这样旋转27次,就是这样的9个弧长的总长.
解答:解:∵菱形ABCD中,AB=2,∠B=60°,
∴△ABC是等边三角形,
∴OA=OC=1,
∴OB= =
= ,
,

第一次旋转的弧长为: =
= π;
π;
第二次旋转的弧长为: =
= π;
π;
第三次旋转的弧长为: =
= ,
,
故可得旋转27次菱形中心O所经过的路径总长=9( π+
π+ π+
π+ )=(6
)=(6 +3)π.
+3)π.
故答案为:(6 +3)π.
+3)π.
点评:本题主要考查了弧长的计算公式以及菱形的性质,根据已知得出菱形每转动3次一循环进而得出经过路径是解题的关键.
(2)从图中可以看出,第一次旋转是以点B为圆心,那么菱形中心旋转的半径就是OB,解直角三角形可求出OB的长,圆心角是60°,第二次还是以点B为圆心,那么菱形中心旋转的半径就是OB,圆心角是60°,第三次就是以点C为旋转中心,OC为半径,旋转的圆心角为60°,旋转到此菱形就又回到了原图,故这样旋转27次,就是这样的9个弧长的总长.
解答:解:∵菱形ABCD中,AB=2,∠B=60°,
∴△ABC是等边三角形,
∴OA=OC=1,
∴OB=
 =
= ,
,
第一次旋转的弧长为:
 =
= π;
π;第二次旋转的弧长为:
 =
= π;
π;第三次旋转的弧长为:
 =
= ,
,故可得旋转27次菱形中心O所经过的路径总长=9(
 π+
π+ π+
π+ )=(6
)=(6 +3)π.
+3)π.故答案为:(6
 +3)π.
+3)π.点评:本题主要考查了弧长的计算公式以及菱形的性质,根据已知得出菱形每转动3次一循环进而得出经过路径是解题的关键.

练习册系列答案
相关题目
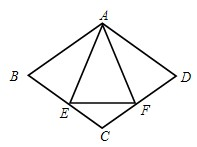 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
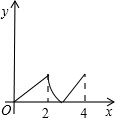
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
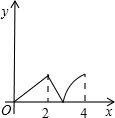
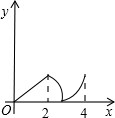
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )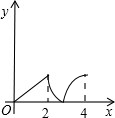
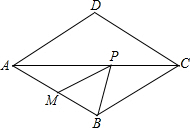 如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2
如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2 如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.
如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm. 如图,菱形ABCD中,∠ADC=120°,AB=10,
如图,菱形ABCD中,∠ADC=120°,AB=10,