Question

1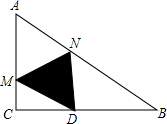．如图，△ABC是一张直角三角形纸片，其中∠C=90°，BC=8cm，AB=10cm，将纸片折叠，使点A恰好落在BC的中点D处，折痕为MN．
（1）求DC的长；
（2）求AM的长．

Answer 1

分析 （1）根据中点的定义可求得DC的长；
（2）在Rt△ACB中，由勾股定理求得求得AC的长，设AM的长为xcm，则CM=6-x，由翻折的性质可知AM=MD=x，最后利用勾股定理列方程求解即可．

解答 解：（1）∵D是BC的中点，BC=8cm，
∴DC=4cm．
（2）在△ABC中，∠C=90°，
∴AC²+BC²=AB²．
∴8²+AC²=10²．
解得：AC=6．
设AM的长为xcm，则CM=6-x，由翻折的性质可知AM=MD=x．
在Rt△MCD中，由勾股定理得：CM²+DC²=DM²，解得：（6-x）²+4²=x²，
解得；x=$\frac{13}{3}$．
∴AM=$\frac{13}{3}$．

点评 本题主要考查的是翻折的性质、勾股定理的应用，利用翻折的性质和勾股定理列出关于x的方程是解题的关键．