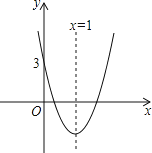��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У��������¶���:��֪�����������������������Ա���![]() ,������������Ӧ�ĺ���ֵ��Ϊ
,������������Ӧ�ĺ���ֵ��Ϊ![]() , ���е�
, ���е�![]() �͵�
�͵�![]() ���ڵ�
���ڵ�![]() �����ĶԳ�(������������غ�)�����ڶԳ�����
�����ĶԳ�(������������غ�)�����ڶԳ�����![]() ����ֱ��
����ֱ��![]() �ϣ����Գ�����������Ϊ����ֱ��
�ϣ����Գ�����������Ϊ����ֱ��![]() �ġ�����������������:
�ġ�����������������: ![]() ��
��![]() Ϊ����ֱ��
Ϊ����ֱ��![]() �� ������������.
�� ������������.
��1����֪��![]() ��ֱ��
��ֱ��![]() ��һ�㣬�������
��һ�㣬�������![]() ���ڵ�
���ڵ�![]() �����ĶԳƵĵ�
�����ĶԳƵĵ�![]() ������:
������:
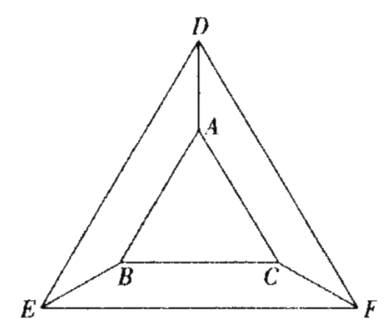
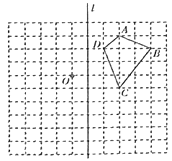
��2����ֱ��![]() ��������ֱ��
��������ֱ��![]() �ġ�������������ͼ����
�ġ�������������ͼ����![]() ��Χ�ɵ������ε����Ϊ
��Χ�ɵ������ε����Ϊ![]() ����
����![]() ��ֵ;
��ֵ;
��3���������![]() ��
��![]() Ϊ����ֱ��
Ϊ����ֱ��![]() �ġ�����������.
�ġ�����������.
�������![]() ��ֵ;
��ֵ;
����֪��![]() ����
����![]() ����
����![]() ֱ��д��
ֱ��д��![]() ��
��![]() �������������߶�
�������������߶�![]() ��Ŀֻ��������ռʱ��Ӧ��
��Ŀֻ��������ռʱ��Ӧ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���𰸡���1����1��-4������2��![]() ����3����-1��2 �� ��
����3����-1��2 �� ��![]() ��
��![]()
��������
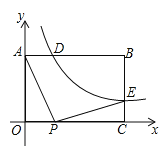
��1���������M�����꣬���ݵ�M���N����![]() �����ĶԳƣ����������N�����ꣻ
�����ĶԳƣ����������N�����ꣻ
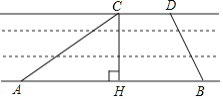
��2�����![]() �͵�
�͵�![]() �ֱ���ֱ��
�ֱ���ֱ��![]() �����ġ�������������ͼ���ϵ�����һ�㣬�������������Ķ��壬�ɵã�ֱ��
�����ġ�������������ͼ���ϵ�����һ�㣬�������������Ķ��壬�ɵã�ֱ��![]() ����ֱ��y=x�����������ǣ�
����ֱ��y=x�����������ǣ�![]() ����ϡ�ֱ��
����ϡ�ֱ��![]() ��������ֱ��
��������ֱ��![]() �ġ�������������ͼ����
�ġ�������������ͼ����![]() ��Χ�ɵ������ε����Ϊ
��Χ�ɵ������ε����Ϊ![]() �����г�����n�ķ��̣�������⣻
�����г�����n�ķ��̣�������⣻
��3���������������Ķ��壬�ã�![]() ����������������⣻�ڷ���������������κ���
����������������⣻�ڷ���������������κ���![]() ��
��![]() ��ͼ���ɵõ��𰸣�
��ͼ���ɵõ��𰸣�
��1���ߵ�![]() ��ֱ��
��ֱ��![]() ��һ�㣬
��һ�㣬
��![]() ������
������![]() ��
��
�ߵ�N���![]() ����
����![]() �����ĶԳƣ�
�����ĶԳƣ�
��![]() ��
��
��2�����![]() �͵�
�͵�![]() �ֱ���ֱ��
�ֱ���ֱ��![]() �����ġ�������������ͼ���ϵ�����һ�㣬
�����ġ�������������ͼ���ϵ�����һ�㣬
��![]() ��
��
![]() ��
��
��ֱ��![]() ����ֱ��y=x�����������ǣ�
����ֱ��y=x�����������ǣ�![]() ��
��
����![]() ����ã�
����ã�![]() ��
��
��ֱ��![]() ��ֱ��
��ֱ��![]() �Ľ���ĺ�����Ϊ
�Ľ���ĺ�����Ϊ![]() ��
��
��ֱ��![]() ��ֱ��
��ֱ��![]() ��y��Ľ�������ֱ��ǣ�(0��n)��(0��-n)��
��y��Ľ�������ֱ��ǣ�(0��n)��(0��-n)��
������ã�![]() ����ã�
����ã�![]() ��
��
��3����������ã�![]() ��
��
��![]() �����������x��������
�����������x��������
��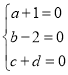 ����ã�
����ã�![]() ��
��
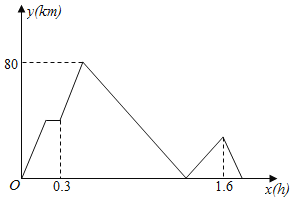
���ɵڢ�С�⣬��֪��![]() ��
��![]() ��
��
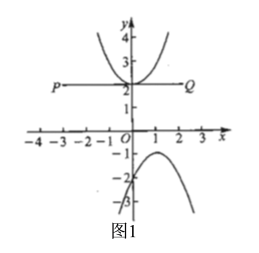
��![]() ʱ����ͼ1��
ʱ����ͼ1��
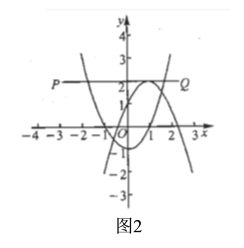
��![]() ʱ����ͼ2��
ʱ����ͼ2��
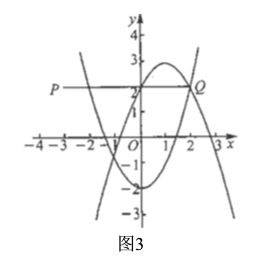
��![]() ʱ����ͼ3��
ʱ����ͼ3��
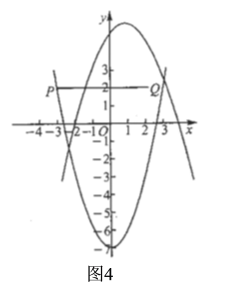
��![]() ʱ����ͼ4��
ʱ����ͼ4��
���Ͽ�֪:![]() ��
��![]() ʱ�����������߶�
ʱ�����������߶�![]() ����ֻ���������㣮
����ֻ���������㣮