题目内容
3.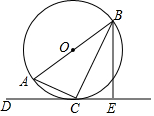 AB是⊙O的直径,CD切⊙O于点C,BE⊥CD于E,连接AC、BC.
AB是⊙O的直径,CD切⊙O于点C,BE⊥CD于E,连接AC、BC.(1)求证:BC平分∠ABE;
(2)若⊙O的半径为3,BE=4,求AC、BC的长.
分析 (1)连接OC,由于CD是⊙O的切线,所以∠OCD=90°,所以易证:∠OCD=∠BED,由于∠OCB=∠OBC,所以BC平分∠ABE;
(2)易证△ABC∽△CBE,从而可知$\frac{AB}{BC}$=$\frac{BC}{BE}$,由于AB与BE的长度可求,所以BC的长度可求出,利用勾股定理即可求出AC的长度.
解答 解:(1)连接OC,
∵CD是⊙O的切线,
∴∠OCD=90°,
∵BE⊥CD,
∴∠BED=90°,
∴∠OCD=∠BED,
∴OC∥BE,
∴∠OCB=∠CBE
∵OC=OB,
∴∠OCB=∠OBC,
∴∠CBE=∠OBC,
∴BC平分∠ABE;
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠BEC,
∵∠ABC=∠CBE,
∴△ABC∽△CBE,
∴$\frac{AB}{BC}$=$\frac{BC}{BE}$,
∴BC2=AB•BE,
∵AB=6,BE=4,
∴BC=2$\sqrt{6}$,
在Rt△ACB中,
∴由勾股定理可知:AC=2$\sqrt{3}$
点评 本题考查圆的综合问题,涉及切线的性质,相似三角形的性质与判定,勾股定理等知识,本题属于中等题型.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
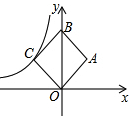 如图,在平面直角坐标系中,正方形OABC的面积为24,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k=-12.
如图,在平面直角坐标系中,正方形OABC的面积为24,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k=-12.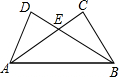 已知:如图,AD=BC,AC=BD.猜想AE与BE的数量关系并证明.
已知:如图,AD=BC,AC=BD.猜想AE与BE的数量关系并证明. 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1,、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2017A2018B2017的面积是24031.
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1,、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2017A2018B2017的面积是24031. 如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.
如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O的半径,且OA=3.